Exponential and Log Functions

Logarithms
First we discuss the inverse function of an exponential function , the so called logarithm
function. It follows from arguments like those above that an exponential function a^x with a >0, is
increasing if and only if a > 1, and is decreasing if a < 1. The exponential function 1^x is neither
increasing nor decreasing, but a constant equal to 1, and has no inverse. However for all a > 0 and
a ≠ 1, the function a^x has an inverse function called the log base a, written 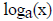. To find the
domain of the log function we must determine the values of the exponential function, so we
assume for ease that a > 1. Then notice that if say a = 1+h where h > 0, then for all positive
integers n, we have 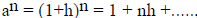with all terms positive , so aⁿ > 1+nh. Since the
right hand side grows to infinity as n does, we conclude that a^x gets arbitrarily large for large x,
i.e. the limit of a^x is +∞ as x approaches +∞. Since 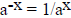, we see that a^x approaches zero
from above as x approaches -∞. Thus a^x assumes all positive values as x ranges over all reals, so
the domain of the inverse function 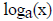is the positive reals . Moreover 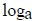is also continuous
and satisfies the law 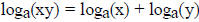for all positive reals x , y, opposite to the law for
the exponential function. Since a function determines its inverse, we have the analogous theorem
to recognize a log function.

Theorem: If g is a non constant continuous function defined for all positive reals, satisfying
1) g(1)= 0, and
2) g(xy) = g(x) + g(y), for all positive x, y,
then there is a unique a > 0 with g(a) = 1, and 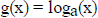, for all positive x.

Now all we have to do is find a differentiable function g satisfying the conditions in the theorem,
and then it must be a log function. if we find one with g(2) = 1, it will prove that 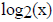is
differentiable. Moreover by the inverse function theorem it will follow that 2^x is also
differentiable, and we will have accomplished by a very indirect route, the goal of proving this
which we temporarily gave up on earlier.

The only tool we have for constructing differentiable functions is the fundamental theorem of
calculus, which allows us to construct a function with any given continuous derivative. Thus in
order to construct a log function we need to know the derivative of a log function. Using the
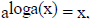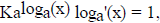chain rule we have so so 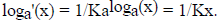Thus
assuming they are differentiable, a log function must have derivative equal to 1/Kx. Now with
this information, we can construct a differentiable function with derivative 1/Kx, and ask
whether it is a log function, which we have every right to expect to be true. Moreover the
simplest choice for k is obviously 1, so we begin from that choice.

Define 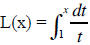. We claim L(x) is a log function. To check this we must show that L(1) = 0
(which is obvious), then that L is continuous, which is always true for a function defined by an
integral, indeed by the FTC this one is even differentiable with derivative 1/x, and finally that
L(xy) = L(x) + L(y) for all x,y > 0. To prove this last formula we use the MVT . I.e. fix y > 0
and let g(x) = L(xy). Then g'(x) = yL'(xy) = y(1/xy) = 1/x = L'(x). Thus L and g have the same
derivative so must differ by a constant according to the MVT. I.e. g(x) = L(xy) = L(x) + c for
some c. To evaluate c, set x = 1 and get L(y) = L(1) + c = c. So c = L(y) and thus L(xy) = L(x) +
L(y) as claimed.

To see what the base is we must find the unique positive number a such that L(a) = 1.
This is not so immediate, but one can show using approximations of the integral that the base is a
number we shall call e such that 2.71828 < e < 2.71829. Indeed since the midpoint estimate is an
underestimate for a function like 1/x which is concave up, using the midpoint estimate on the
interval [1,3] we get L(3) ≥ 2(1/2) = 1, so e ≤ 3. Subdividing into [1,2] and [2,2.8] we have
midpoint estimate 2/3 + 5/12 = 13/12 ≤ L(2.8), so e < 2.8. Then using the trapezoidal upper
estimate for the subdivision [1,1.4], [1.4,1.8] and [1.8,2.2], [2.2,2.6] gives (1/5)(1 + 10/7 + 10/9
+10/11 + 5/13) ≤ (1/5) (1 + 1.43 + 1.112 + .9091 + .385) ≤ .97. Thus e > 2.6. Later we will find
a better way to estimate e using infinite series.

We see that 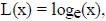but it is usual to write it as ln(x). In particular ln(x) is a
differentiable function defined on all positive reals , with derivative 1/x, and which takes on all real
values . Its inverse is the exponential function e^x whose derivative is also e^x. If K = ln(2) and if
we consider the function 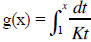, it follows from the same argument as above using MVT,
that g is a logarithm function. The base is the unique number a such that g(a) = 1. But since g(x)
= (1/K)ln(x) = ln(x)/ln(2), it follows that this number is 2. Hence 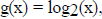, and we see the
derivative of g is 1/(ln(2)x). Using the inverse function theorem, the inverse of g is the
differentiable function f(x) = 2^x with derivative f'(x) = ln(2) 2^x.
We obtain as well that for all a > 0, the function 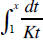where K = ln(a), is the
differentiable log function . Its inverse is then the differentiable function a^x, with
derivative ln(a) a^x. In fact, for all a > 0, we can express a^x in terms of e^x, by using the corollary
above to write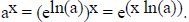

Now that we have definition and the basic properties of exponential and log functions, the other
basic properties are their rates of growth. According to the formulas above we can express every
exponential function in terms of the simplest one e^x, so we may consider only that one. Similarly
we saw above that for all a > 0, that 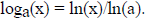Basically e^x grows rapidly, faster than
any positive power of x , and ln(x) grows slowly, slower than any positive power of x.
More precisely , for all r > 0, we have 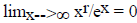, and .
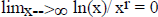There are several ways to prove this, but the easiest way, and the way which teaches us the most
useful fact, is to use l'Hopital's rule.

Theorem: If f, g are both differentiable functions such that both have limit ± ∞, or if both have
limit 0, as x approaches a, or as x approaches ∞, then the limit of f/g equals the limit of f'/g',
assuming that latter limit exists.

Using this theorem on 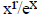, we can take derivatives until the power of x in the top is non
positive, so that then the function in the top is constant or approaches zero as x approaches
infinity, and the one in the bottom, still equal to e^x, approaches infinity. Then the limit is 1/∞, or
0/∞, both = 0. For the limit 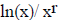, one can begin with ln(x)/x and take one derivative in top and
bottom to finish. Then for the general case, one may consider instead the equivalent limit
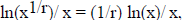which we have already done. (The only point is that the bottom
number should be the rth power of the top number, and that both approach infinity, it does not
matter which one we call x.)