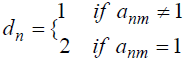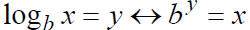Functions
• Domain: set which holds the values to which we
apply the function
• Co-domain: set which holds the possible values
(results) of the function
• Range: set of actual values received when applying
the function to the values of the domain
Function
• A “total” function is a relationship between elements of
the
domain and elements of the co-domain where each and
every element of the domain relates to one and only one
value in the co-domain
• A “partial” function does not need to map every element
of
the domain.
• f: X →Y
– f is the function name
– X is the domain
– Y is the co-domain
– x ∈X y ∈Y f sends x to y
– f(x) = y f of x ; value of f at x ; image of x under f
Formal Definitions
• Range of f = {y ∈Y | ∃x ∈X,
f(x) = y}
– where X is the domain and Y is the co-domain
• Inverse image of y = {x ∈X| f(x) = y}
– the set of things that map to y
• Arrow Diagrams
– Determining if they are functions using the
Arrow Diagram
Teminology of Functions
• Equality of Functions
∀f,g
∈{functions}, f=g ↔ ∀x∈X,
f(x)=g(x)
• F is a One-to-One (or Injective) Function iff
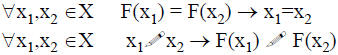
• F is NOT a One-to-One Function iff
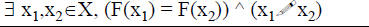
• F is an Onto (or Surjective) Function iff
∀y
∈Y
∃x∈X,
F(x) = y
• F is NOT an Onto Function iff
∃y∈Y
∀x
∈X, F(x)
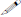 y
y
Proving functions
one-to-one and onto
f:R→R
f(x)=3x-4
• Prove or give a counter example that f is one-to-one
use
def: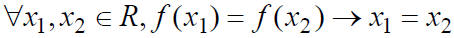
• Prove or give a counter example that f is onto
use
def:
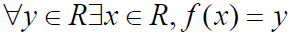
One-to-One Correspondence
or Bijection
F:X →Y is bijective ↔ F:X →Y is one-to-one & onto
• F:X →Y is bijective ↔ It has an inverse function
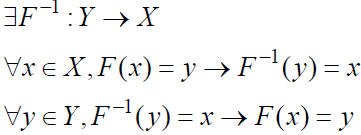
Proving something is a bijection
• F:Z→Z
F(x)=x+1
• Prove it is one-to-one
• Prove it is onto
• Then it is a bijection
• So it has an inverse function
– find F-1
Pigeonhole Principle
• Basic Form
A function from one finite set to a smaller finite
set cannot be one-to-one; there must be at least
two elements in the domain that have the same
image in the co-domain.
Examples
• Using this class as the domain,
Must two people share a birthmonth?
Must two people share a birthday?
• A = {1,2,3,4,5,6,7,8}
If I select 5 integers at random from this set,
must two of the numbers sum to 9?
If I select 4 integers?
Other (more useful) Forms of the
Pigeonhole Principle
• Generalized Pigeonhole Principle
– For any function f from a finite set X to a finite set Y and for any
positive integer k, if n(X) > k*n(Y), then there is some y ∈Y
such that y is the image of at least k +1 distinct elements of X.
• Contrapositive Form of Generalized Pigeonhole Principle
– For any function f from a finite set X to a finite set Y and for any
positive integer k, if for each y ∈Y, f-1(y) has at most k elements,
then X has at most k*n(Y) elements.
Examples
• Using Generalized Form:
– Assume 50 people in the room, how many must share the same
birthmonth?
– n(A)=5 n(B)=3 F:P(A)→P(B)
How many elements of P(A) must map to a single element of P(B)?
• Using Contrapositive of the Generalized Form:
– G:X→Y where Y is the set of 2 digit integers that do not have
distinct digits. Assuming no more than 5 elements of X can map
to a single element of Y, how big can X be?
– You have 5 busses and 100 students. No bus can carry over 25
students. Show that at least 3 busses must have over 15 students
each.
Composition of Functions
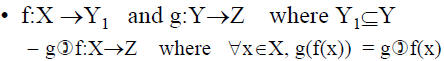
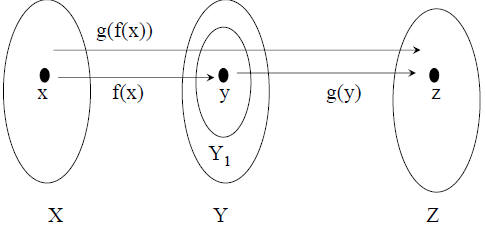
Composition on finite sets
• Example
– X = {1,2,3} Y1 = {a,b,c,d} Y={a,b,c,d,e} Z =
{x,y,z}
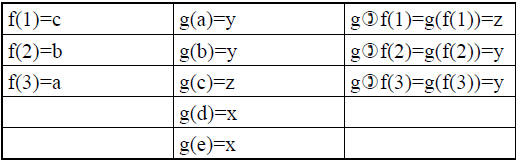
Composition for infinite sets
f:Z →Z
f(n)=n+1
g:Z →Z
g(n)=n2
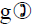 f(n)=g(f(n))=g(n+1)=(n+1)2
f(n)=g(f(n))=g(n+1)=(n+1)2
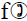 g(n)=f(g(n))=f(n2)=n2+1
g(n)=f(g(n))=f(n2)=n2+1
note:
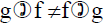
Identity function
•
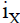 the identity function for the domain X
the identity function for the domain X
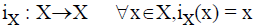
•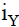 the identity function for the domain Y
the identity function for the domain Y
• composition with the identity functions
Composition of a function with
its inverse function
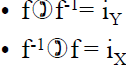
• Composing a function with its inverse
returns you to the starting place.
(note: f:X→Y and f-1: Y→X)
One-to-One in Composition
• If f:X→Y and g:Y→Z are both one-to-one,
then
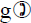 f:X→Z is one-to-one
f:X→Z is one-to-one
• If f:X→Y and g:Y→Z are both onto,
then
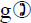 f:X→Z is onto when Y = Y1
f:X→Z is onto when Y = Y1
Cardinality
• Comparing the “sizes” of sets
– finite sets ( or has a bijective function from it to
or has a bijective function from it to
{1,2,…,n})
– infinite sets (can’t have a bijective function from it to
{1,2,…,n})
•
∀A,B ∈{sets}, A and B have the same cardinality
↔ there is a one-to-one correspondence from A to B
In other words,
Card(A) = Card(B) ↔∃ f ∈{functions}, f:A→B ∧ f is a
bijection
Countability of sets of integers
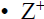 is a countably infinite set
is a countably infinite set
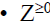 is a countably infinite set
is a countably infinite set
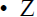 is a countably infinite set
is a countably infinite set
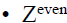 is also a countably infinite set
is also a countably infinite set
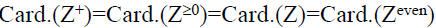
• We’ll take just a part of this infinite set
• Reals between 0 and 1 (non-inclusive)
– X = {x ∈ R| 0<x<1}
• All elements of X can be written as
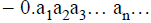
Cantor’s Proof
• Assume the set X = {x∈R|0<x<1} is countable
• Then the elements in the set can be listed
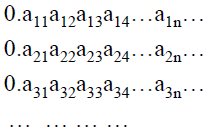
• Select the digits on the diagonal
• d differs in the nth position from the nth in the list
All Reals
• Card.({x∈R|0<x<1} ) = Card.(R)
Positive Rationals Q +
• Card.(Q+) =?= Card.(Z)
log function properties
(from back cover of textbook)
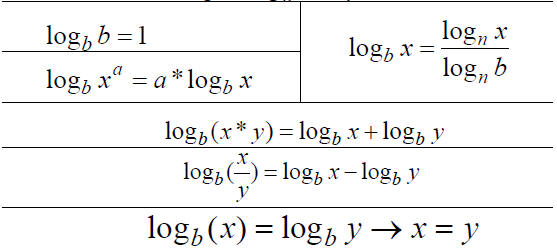
| Prev | Next |