Polynomial Division , The
Remainder Theorem, and The
Factor Theorem

Long Division

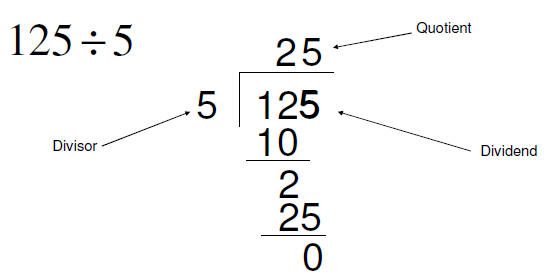
Notice: If we get a remainder of zero the quotient is a factor of the dividend

We have known how to find factors of integers using division for years

We can use long division on polynomials in a like manner

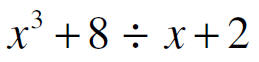
Set-up Put the divisor outside

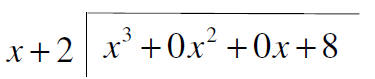Put the dividend inside with
every degree of the variable shown

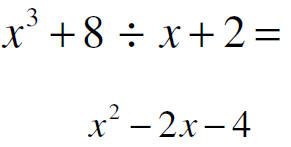
Warning: This book may represent the remainder as some function
R(x) and say R(x) = (some constant.)
 

ONLY if we write the QUOTIENT as the sum of two separate functions
would this be acceptable.
Otherwise the answer is as shown as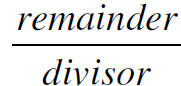

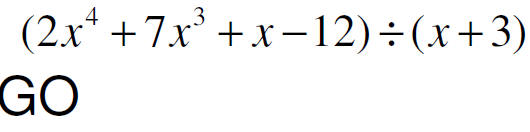
Synthetic Division

• Can only use when the divisor has a degree of 1. Otherwise a different method is needed .

• Uses the coefficients

• Must backfill for all powers of the variable

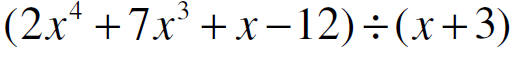
Set-up Put the solution outside
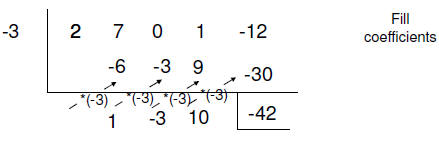The 1st coefficient moves down
Multiply by solution and move	Add

The numbers below the line are the coefficients to a term that is lower by 1 degree

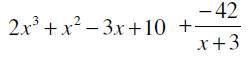
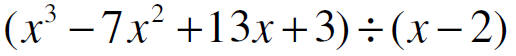
GO

The remainder Theorem

• If a number c is substituted for x in the polynomial p(x)

• then the result p(c) is the remainder that would result from dividing p(x) by (x-c)

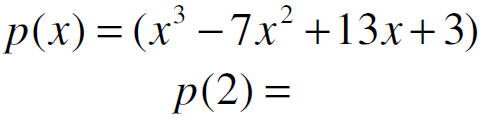
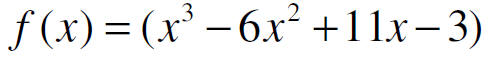
Find the remainder for: f(1) f(3) f(-2)

Check with synthetic division

The Factor Theorem

• For a polynomial p(x)

• if p(c) = 0

• then (x-c) is a factor of p(x)

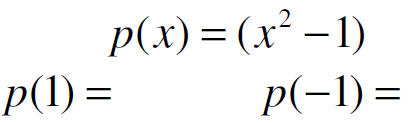
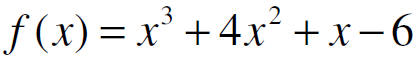
Test the following numbers to see if they are zeros using
the table feature in the calculator
1, -2, 3
If they are zeros, give the factors