Polynomials
The Degree of axn
• If a does not equal 0,the degree of axn
is n.
The degree of a nonzero constant is 0.The
constant 0 has no defined degree.
Definition of a Polynomial in x
• A Polynomial in x an algebraic
expression of the form
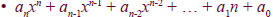
• Where 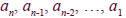 and
and 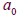 are real
are real
numbers.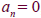 ,and n is a non-negative
,and n is a non-negative
integer. The Polynomial is of degree n, an
is the leading coefficient, and 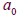 is the
is the
constant term.
Text Example
Perform the indicated operations and simplify :
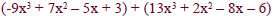
Solution
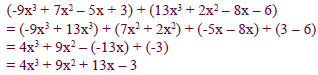
Group like terms .
Combine like terms .
Multiplying Polynomials
The product of two monomials is obtained by using
properties of exponents .
For example
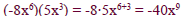
Multiply coefficients and add exponents.
Further more , we can use the distributive property to
multiply a monomial and
a polynomial that is not a monomial . For example,
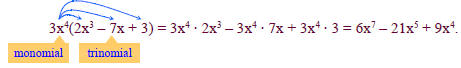
Multiplying Polynomials When
Neither is Monomial
• Multiply each term of one polynomial by
each term of the other polynomial. Then
combine like terms.
Using the FOIL Method to Multiply Binomials
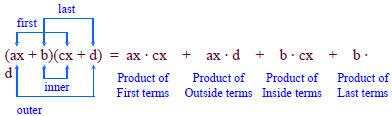
Text Example
Multiply: 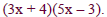
Solution:
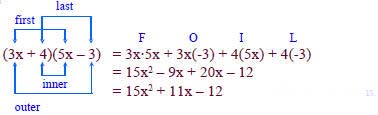
Combine like terms.
The product of the Sum and
Difference of Two Terms
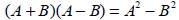
• The product of the sum and the difference
of the same two terms is the square of the
first term minus the square of the second
term.
The Square of a Binomial Sum
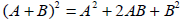
• The square of a binomial sum is the first term
squared plus 2 times the product of the
terms plus last term squared.
The Square of a Binomial
Difference
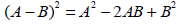
The square of a binomial difference is the first
term squared minus 2 times the product of
the terms plus last term squared.
Special Products
Let A and B represent real numbers , variables , or algebraic expression.
|
Special Products Sum and Difference of Two Terms |
Example |
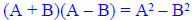 |
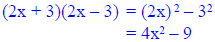 |
| Square a Binomial | |
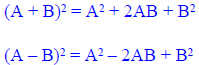 |
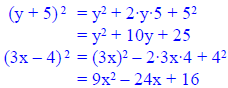 |
| Cubing a Binomial | |
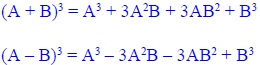 |
 |
Text Example
Multiple: 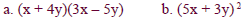
Solution
We will perform the multiplication in part (a) using the
(FOIL) method. We Will
multiply in part (b) using the formula for the square of a binomial,
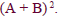
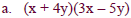 Multiply these
binomial using the FOIL method.
Multiply these
binomial using the FOIL method.
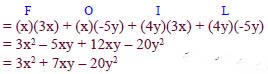 Combine like terms.
Combine like terms.
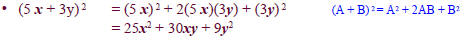
Example
Multiply: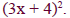
• Solution:
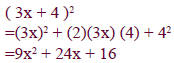
| Prev | Next |