Additional Topics With Rational Numbers

Example 4 Given the sequence, determine whether it is arithmetic or geometric, find the
common difference or common ratio, and find the next term.

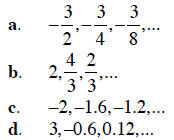
Solution
a. First we need to determine if the sequence is arithmetic or geometric.
Note that:

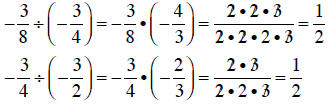
So the sequence is geometric and the common ratio is1/2. The next term is
given by:

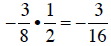
b. First we need to determine if the sequence is arithmetic or geometric .
Note that:

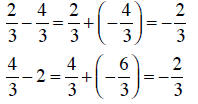
So the sequence is arithmetic and the common difference is . The next
term is given by:

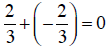
c. First we need to determine if the sequence is arithmetic or geometric.
Note that:

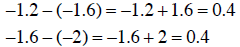
So the sequence is arithmetic and the common difference is 0.4. The next
term is given by:

-1.2 + 0.4 = -0.8

d. First we need to determine if the sequence is arithmetic or geometric.
Note that:

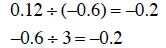
So the sequence is geometric and the common ratio is –0.2. The next term is
given by:

0.12 • (-0.2) = -0.024

We conclude this section with an application of rational numbers which involves order of
operations.

Example 5 Steve owns 120 shares of a stock which rises 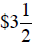per share one day, and 250
shares of a stock which loses 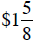per share on the same day. Did he have a net
gain or loss, and how much was it?

Solution Treating the stock rise as a positive number and the stock loss as a negative
number, his net gain or loss is given by:

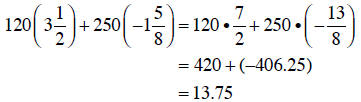
Steve had a slight gain of $13.75 on the day. Note that we converted to decimals
in the second step , since they are commonly used in our dollar money system .

Terminology
graphing inequalities
geometric sequences

arithmetic sequences

Exercise Set 3.6

Replace the blank with the correct symbol : <, =, or >

Graph the given inequality .

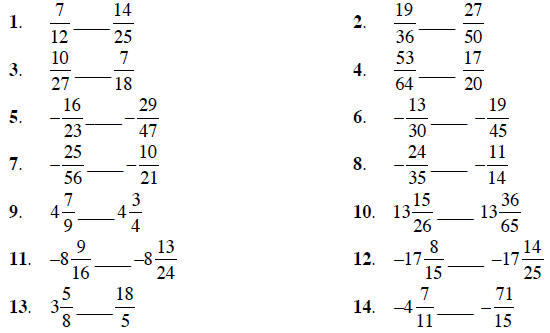
Determine whether or not the given rational number is a solution to the equation .

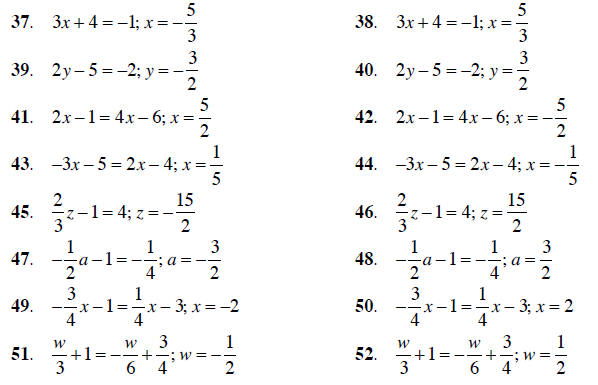
Given the sequence, determine whether it is arithmetic or geometric, find the common difference
or common ratio, and find the next term.

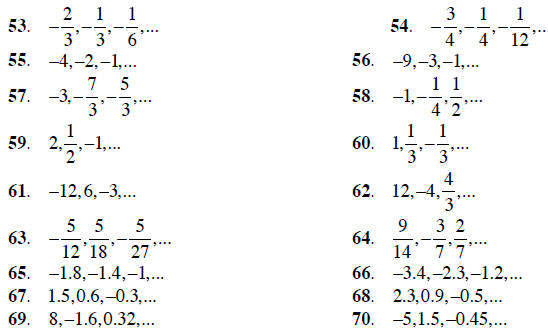
Answer each of the following application questions. Be sure to read the question, interpret the
problem mathematically , solve the problem , then answer the question. You should answer the
question in the form of a sentence.

71. Bernice owns 460 shares of a stock which gains 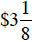per share one day, and 320
shares of a stock which lose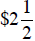s per share that day. Did she have a net gain or loss
that day, and how much was it?

72. Brian owns 360 shares of a stock which gains 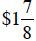per share one day, and 170 shares
of a stock which loses per share that day. Did he have a net gain or loss that day,
and how much was it?

73. Todd signs a two year lease for his new BMW. The lease requires a $2,450 down
payment and payments of $473.58 per month. What is the total amount he paid for the
lease?

74. Brad signs a four year loan for his yacht. The loan requires a $6,500 down payment
and payments of $683.97 per month. What is the total amount he paid for the yacht?

75. Carol signs a 15 year loan for her house. The loan requires a $18,760 down payment
and payments of $1,265.49 per month. What is the total amount she paid for the
house?

76. Tracy signs a 30 year loan for her house. The loan requires a $6,890 down payment
and payments of $732.26 per month. What is the total amount she paid for the house?

77. Jerry’s walnut trees produce 80 pounds of walnuts per tree. He plants 50 trees per acre,
and has 86 acres of walnuts. If Jerry is paid $0.67 per pound for the walnuts, what is
the total revenue from his walnut orchard?

78. During a low production year , Jerry (from Exercise 77) has a yield of only 62 pounds
of walnuts per tree. However, the price paid for the walnuts raises to $0.84 per pound.
Will his total revenue increase or decrease? By how much?

79. You commute to (and from) work 218 times during the year. The distance from your
home to work is 24 miles. If the cost of operating your car is 26 cents/mile, what is
your cost of commuting during the year?

80. Mary commutes to (and from) work 209 times during the year. The distance from her
home to work is 8 miles. If the cost of operating her car is 35 cents/mile, what is her
cost of commuting during the year?

81. Frank’s Cleaners contracts to clean 325 shirts and 130 pairs of pants for one week.
Frank is paid $2.25 for each shirt and $4.25 for each pair of pants. How much is the
weekly contract?

82. A separate contract with Frank’s Cleaners (from Exercise 81) is to clean 286 shirts and
155 pairs of pants for one week. If the amount per shirt and pair of pants remains
unchanged, will this contract be more or less? By how much?