Algebra Homework 3 Solutions
Problem 5: Use four-digit rounding arithmetic and the formulas to find the most
accurate
approximations to the roots of the following quadratic equations . Compute the
relative error.
a)
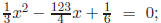
b) 1.002x2 + 11.01x+ 0.01265 = 0.
Solution : The quadratic formula states that the roots of ax2 + bx + c = 0 are
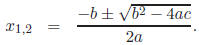
a) The roots of
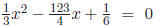 are approximately
are approximately
x1 = 92.24457962731231,
x2 = 0.00542037268770.
We use four- digit rounding arithmetic to find approximations to the roots. We
find the
first root:
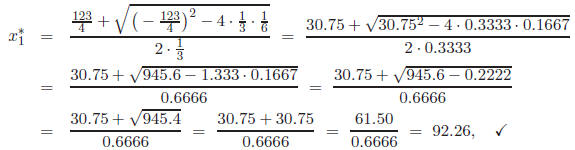
which has the following relative error:
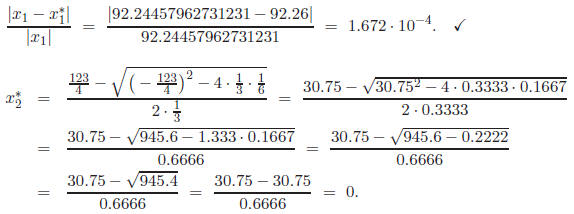
has the following relative error:
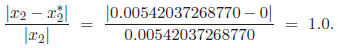
We obtained a very large relative error, since the
calculation for
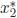 involved the subtraction
involved the subtraction
of nearly equal numbers . In order to get a more accurate approximation to
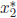 , we need
, we need
to use an alternate quadratic formula , namely
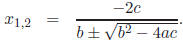
Using four- digit rounding arithmetic, we obtain:
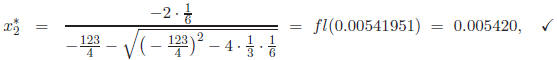
which has the following relative error:
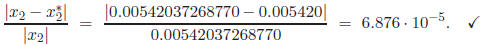
b) The roots of 1.002x2 + 11.01x+ 0.01265 = 0 are approximately
x1 = −0.00114907565991,
x2 = −10.98687487643590.
We use four-digit rounding arithmetic to find approximations to the roots.
If we use the generic quadratic formula for the calculation of
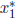 , we will encounter the
, we will encounter the
subtraction of nearly equal numbers (you may check). Therefore, we use the
alternate
quadratic formula to find
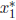 ;
;
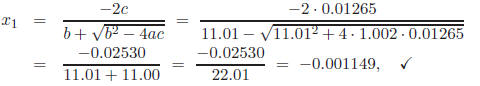
which has the following relative error:
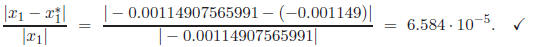
We find the second root using the generic quadratic formula :
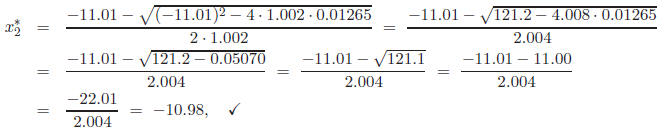
which has the following relative error:
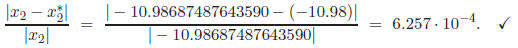
Similar Problem
The roots of 1.002x2 − 11.01x+ 0.01265 = 0 are approximately
x1 = 10.98687487643590,
x2 = 0.00114907565991.
We use four-digit rounding arithmetic to find approximations to the roots. We
find the
first root:
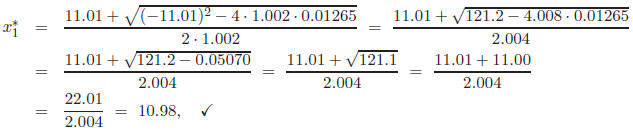
which has the following relative error:
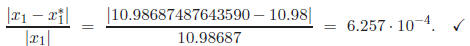
If we use the generic quadratic formula for the
calculation of
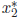 , we will encounter the
, we will encounter the
subtraction of nearly equal numbers. Therefore, we use the alternate quadratic
formula
to find
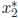 :
:
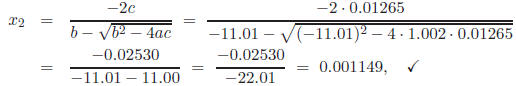
which has the following relative error:
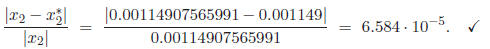
Problem 6: Suppose that fl(y) is a k-digit rounding approximation to y. Show that
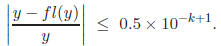
(Hint: If
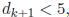 then
then
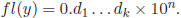
If
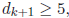 then
then
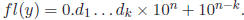 )
)
Solution : We have to look at two cases separately.
Case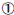 :
:
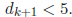
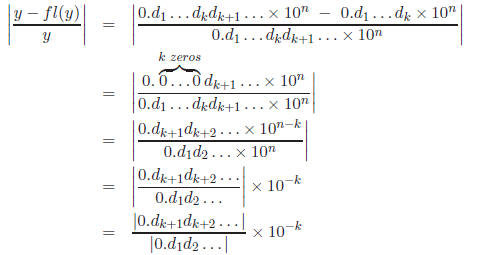
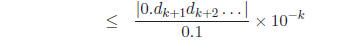 since
since
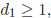 so
so

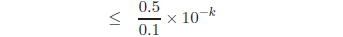 since
since
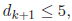 by assumption
by assumption
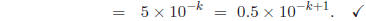
Case
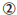 :
:
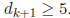
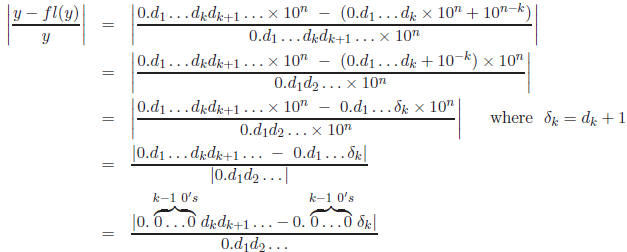
Note that 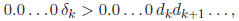
and 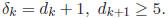
For example, 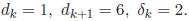
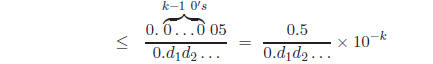 since
since
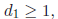 so
so 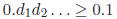
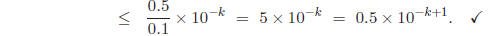
| Prev | Next |