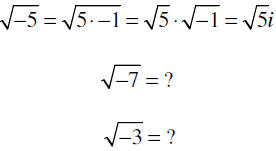Complex Numbers
| Section 1.3 Complex Numbers |
| How can we solve the equation x 2= −1? x = ± 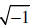 It turns out that this is not a real number ! So we have to "make up " some new numbers! We define the new number i as follows i = |
| Complex Numbers Let i2=-1 then i= i is the square root of -1 |
| Examples
|
| Complex Numbers A complex number has the form a + bi a is called the real part of the complex number b is called the imaginary part of the complex number |
The Complex Plane |
| Adding Complex Numbers (a + bi ) + (c + di ) = (a + c) + (b + d ) i To add two complex numbers, add the real parts and add the imaginary parts, the result is a complex number. |
| Examples (2 + 3i ) + (−5 + 4i ) = (5 + 2i ) − (2 − 7i ) = |
| Multiplying Complex Numbers (a+bi ) (c+di ) = ac + adi + bci + bdi2 = (ac −bd ) + (ad + bc) i This fol lows from the distributive property and the fact that t2 = −1 |
| Examples (2 + 3i ) (−5 + 4i ) = (5 + 2i ) (2 − 7i ) = (a + bi ) (a − bi ) = ( a + bi) and (a − bi ) are called complex conjugates |
| If z=a + bi is a complex number, then 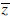 = a -bi is the
conjugate of z. = a -bi is the
conjugate of z.The product of a complex number and its conjugate is a real number.  |
| Multiply the complex conjugates (2 + 3i ) (2 − 3i ) = (5 − 2i ) (5 + 2i ) = (c + di ) (c − di ) = |
Dividing Complex Numbers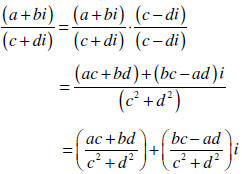 |
| Magnitude of Complex Numbers If c = a + bi is a complex number, The absolute value (magnitude) of is the distance away from 0 0 in the complex plane. 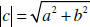 This follows from the distance formula! |
The Complex Plane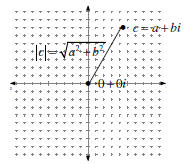 |
| Examples Find 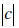 c = 2 + 3i c = 5 − 4i c = −4 + 3i c = −4 − 3i |
| The Quadratic Formula If ax2 + bx + c = 0 then 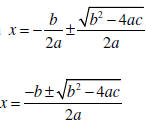 |
| Use the quadratic formula to solve x2 + 4 = 0 3y2 + 2y +1= 0 2t2− t = −2 |
| Analytical Solutions Given a quadratic equation ax 2 + bx + c = 0 Use the quadratic formula 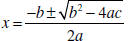 If b 2− 4ac > 0 there are two real solutions If b2 − 4ac = 0 there is one real solution If b2 − 4ac< 0there are no real solutions, but two complex conjugate solutions. |
| Prev | Next |