Computer Science 1110 Exam

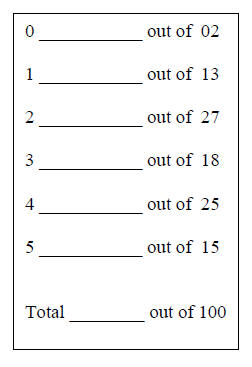
This 90-minute exam has 6 questions (numbered 0..5) worth a total of 100 points. Spend a few minutes
looking at all the questions before beginning. Use the back of the pages if you need more space.

Question 0 (2 points). Fill in the information, legibly, at the top of each page. (Hint: do it now.)

Question 1 (13 points). Arrays and methods .

Below to the left is a square array . Write a method that turns such an array into its transpose, which is
shown to the right. The transpose of a square array arises from switching rows and columns. If the array is
the pixels in an image, then transposing the image turns it on its side.

You do not have to write loop invariants, although the practice of writing an invariant for a loop and
stating in a comment at the beginning of the repetend what the repetend does increases programming effectivity.
And if you want to swap b[h] and b[k], just say that instead of writing it in Java.

/** = Change m into its transpose.
Precondition: m is not null and is square (the number of rows = the number of columns) */
public static void transpose (int[][] m) {

Question 2 (27 points). Miscellaneous
(a) Write a single statement that declares and initializes a two-dimensional int array b to look like the
table that appears to the right

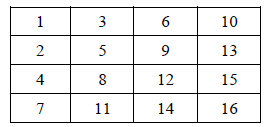
(b) To the right is a class definition. Below are 5 statements. Draw the
variables that are declared in the statements. Then, execute the statements
one by one, in order , drawing any objects that are created during execution
and storing values in appropriate variables when an assignment is executed.
When storing a value in a variable , cross out, do not erase, the old value.

C h= new C(3, 1);
C k= new C(5, 6);
C j= h;
j.x= j.x + 1;
j.y= h.x + h.y;

public class C {
public int x;
public int y;
public C(int a, int b) {
x= a; y= b;
}
}

(c) Any positive integer can be reduced to a single digit by repeatedly adding its digits together until the
result is < 10. For example, change 257 to 25 + 7 and then to 7 + 7 and then to 14 and finally to 5. Or do
it this way: change 257 to 2 + 57 and then to 2 + 12 and then to 2 + 3 and then to 5. Or, try 257 -> 25 + 7
-> 32 -> 5. There are other ways to do it. Write the following recursive function. Do not use a loop, and
do not introduce Strings

/** = n reduced to a single digit (by repeatedly adding its digits. Precondition: n > 0 */
public static int addUp (int n) {

Question 3 (18 points) Below is a class Rational. Complete the bodies of the constructor, and functions
toString and equals. Read the whole class, all of its methods, before doing anything.

/** An instance is a rational number */
public class Rational {
/** Class invariant: the rational number is num / den
Restrictions on fields: 1. den > 0
2. if num = 0, then den = 1
3. num / den is in lowest possible terms.
E.g. instead of 20/8 or –5/10, these rational numbers are stored as 5/2 and –1/2. */
private int num;
private int den;
/** Constructor: an instance with rational number n / d.
Precondition: d != 0 */
public Rational(int n, int d) {

}
/** = the numerator */
public int getNumerator() { return num; }
/** = the denominator */
public int getDenominator() { return den; }
/** = a representation of this rational number, in the form num/den. */
public String toString() {

}
/** = "r is of class Rational and has the same value as this Rational number”. */
public boolean equals(Object r) {

}
/** Change num and den so that this rational number is in the lowest possible terms,
e.g. 8/24 becomes 1/3. */
private void reduce(){
You do not have to write this procedure.
}
}

Question 4. (25 points). Vector v may contain instances of many different classes, e.g. Rational (see
question 3), Integer, Double, and others. There may be duplicates in v —for example, two instances of
Rational in class v may contain the same rational number. We want to write procedures that will remove
duplicates of class Rational from v. By a duplicate, we do not mean the same object; rather, we mean an
object that contains the same rational number.

Below, two procedures are specified. Write their bodies. Do not use recursion.
You must use the invariants P1, and P2, which are given both in English and as
pictures, to write loops (with initialization). Remember our principle to rely on
previously written functions, where possible.

Use v.remove(k)
to remove element
k from v.

/** Remove all Rational elements from v[h..] that have the same value as r.
Precondition: 0 <= h < v.size(). */
public static void removeRationalEquals(Vector v, int h, Rational r) {

// inv P1. No Rational element in
v[h..k-1] has the same value as r */

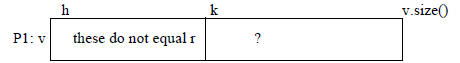
// Postcondition: no Rational element in v[h..] has the same value as r
}

/** Remove all duplicate Rational numbers from v (so that each appears in it only once). */
public static void removeRationalDups(Vector v) {

// inv P2: No Rational instance in v[0..h-1]
has a duplicate in v.*/

Postcondition: No Rational instance in v has a duplicate in v.
}

Question 5 (15 points). Known algorithms.
(a) (10 pts) Write a specification and header for a binary search
function that searches sorted array segment b[p..q-1]. Your
specification may be in terms of pictures , English, mathematical
notation, or a mixture of all of them. But it must be a specification
of binary search as we have presented the algorithm in
class. Note carefully which array segment is to be searched.

(b) (10 pts) Develop the body of the function specified above. When developing the body, write the invariant
for the loop first. Then develop the loop and initialization using the four loopy questions. An
answer that does not have a suitable loop invariant will receive no credit. Note carefully that the
sorted array segment to be searched is b[p..q-1].