Rational Exponents

Notes for R.6 Rational Exponents (pp. 55 – 62)

Topics: Negative and Rational Exponents and Their Properties

I. Negative Exponents and the Quotient Rule (pp.55 – 57)

Recall: The Product Rule for Exponents states that ________

_____________

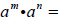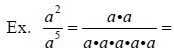So the definition of a negative exponent is that we use the reciprocal of the
____________________________.

*Negative exponents are instructions to rewrite as the reciprocal, not anything left of
zero on the number line .

When we use the Quotient Rule and divide with exponents , we ___________________
_________________________________________________

Special cases:

a⁰ =1 and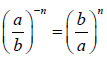

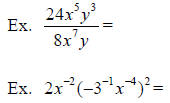
II. Rational Exponents (pp. 58 –61)

Def.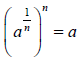, when n is an even positive integer, and when a is positive. Also,
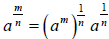is called the _______________ n^th root of a.
Def.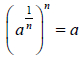, when n is an odd positive integer, and when a is any real number. The
answer is the positive or the negative real number whose n^th power is a.

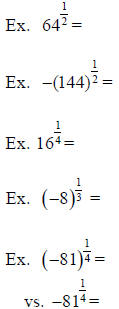
*Note the big difference that the ( ) make in the solutions to these two problems !

For rational exponents with a value other than 1 in the numerator of its exponent, then
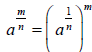or 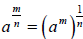, whichever is more convenient.

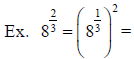or

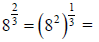
Summary of Exponential Definitions and Rules

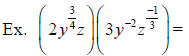
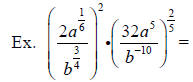
Factoring Polynomials with Rational Exponents: Factor out the smaller exponent.

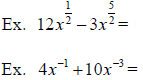
III. Omit More Complex Fractions (p.61) (Stop video at 18:24 – 19:45)

IV. Calculator Notes :
• When entering an exponent in the calculator, use the ^ key or the “to the” key.
Ex. 2³ is entered as “2 ^ 3” and read aloud as “Two to the third power”.
• When entering an exponent that is a fraction , you must use ( ) around the
fraction. Ex. is entered as “2 ^ ( 3 / 4 )”