Mathematics for Elementary Teachers

Course Description:
This course is designed to provide prospective teachers with the knowledge and skills necessary to effectively communicate mathematical concepts. Topics include techniques of problem solving, set theory, number theory, the real number system, elementary algebra, and an introduction to geometry.

Required Text:
Billstein, R.; Libeskind, S.; & Lott, J. W. (2001);
A Problem Solving Approach to Mathematics for Elementary School Teachers, (8^th ed.). Reading, MA; Addison-Wesley Publishing.

Materials:
Scientific calculator
Metric/English ruler
Compass/Protractor
Manipulative Kit (Optional)

Method of Instruction: Lecture

Manuals:
Dolan, D., Williamson, J., & Muri, M. (2004). Mathematics Activities for Elementary School Teachers : A Problem Solving Approach, (5^th ed.) Reading, MA; Addison-Wesley Publishing.

Disclaimer: None

CORE COURSE PERFORMANCE OBJECTIVES

The student will be able to:
1. Demonstrate the ability to teach techniques of problem solving. (CCC1,3,7)
2. Use principles of set theory to solve problems. (CCC 2,7)
3. Use principles of number theory to solve problems. (CCC 2,7)
4. Perform operations using the real number system. (CCC 7)
5. Solve problems using elementary algebra . (CCC 2,7)
6. Define basic geometric terms. (CCC 1,2)

MEASURABLE PERFORMANCE OBJECTIVES

1. Demonstrate the ability to teach techniques of problem solving. (CCC1,1,7)
1.1 Define and describe the four steps of the problem solving process and to use pattern recognition as one of the strategies of problem solving.
1.2 Examine the four steps of the problem solving process and learn to use them in a generalized approach to a variety of problems.

2. Use principles of set theory to solve problems. (CCC 2,7)
2.1 Define and describe logic, negation, logic quantifiers, truth tables, compound statements, conjunction, disjunction, and logical equivalence, and demonstrate their use by solving application problems.
2.2 Define and describe conditional, hypothesis, conclusion, converse, inverse, contrapositive, biconditional, tautology, valid reasoning, direct reasoning, Law of Detachment, indirect reasoning, and the Chain Rule, and demonstrate their
use by solving application problems.
2.3 Define and describe operations on sets, including intersection, union, complement, and Cartesian product , and solve related application problems.
2.4 Define relations, functions and their properties, and solve related application problems.

3. Use principles of number theory to solve problems. (CCC 2,7)
3.1 Use a scientific calculator to solve appropriate problems.
3.2 Develop a greater understanding of our number system by comparing it with other systems developed throughout history.
3.3 Compare and contrast the base ten number system with systems using other bases.
3.4 Convert numbers from one base to another, and perform addition, subtraction, multiplication and division in a non-ten base system.

4. Perform operations using the real number system. (CCC 7)
4.1 Perform addition and subtraction of whole numbers using a variety of models.
4.2 Perform multiplication and division of whole numbers using a variety of models.
4.3 Apply algorithms and use mental arithmetic and estimation to perform whole number addition and subtraction.
4.4 Apply algorithms and use mental arithmetic and estimation to perform whole number multiplication and division.
4.5 Perform addition and subtraction of integers using a variety of models.
4.6 Perform multiplication and division of integers using a variety of models.
4.7 Write and solve equations and inequalities using a variety of models.
4.8 Describe and apply divisibility tests on integers.
4.9 Identify and define prime and composite numbers, and utilize theorems to solve application problems.
4.10 Identify and define greatest common divisor and least common multiple, and demonstrate their use by solving application problems.
4.11 Demonstrate an understanding of congruences in mathematics and modular arithmetic by using the arithmetic of a 12-hour clock and calendars in problem solving.
4.12 Describe and define fraction, rational numbers, numerator, denominator, equivalent fractions, Fundamental Law of Fractions, simplest form of a fraction, and equality of fractions, and demonstrate their use by solving application problems.
4.13 Use the strategies of problem solving and the properties and theorems of addition and subtraction of rational numbers to solve application problems.
4.14 Use the strategies of problem solving and the properties of multiplication and division of rational numbers to solve application problems.
4.15 Define and describe ratio and proportion, and demonstrate their use by solving application problems.
4.16 Define inequality, the Denseness Property, and the related theorems, and demonstrate their use by solving application problems.
4.17 Define and use the properties of exponents with rational numbers to solve application problems.
4.18 Define decimal notation in relation to a base ten system.
4.19 Conversion decimals to fractional forms.
4.20 Use mental and calculator decimal computations to solve application problems involving decimals.
4.21 Define repeating decimals and scientific notation.
4.22 Convert any rational number to a decimal.
4.23 Use rounding and estimating in decimal computations.
4.24 Convert numbers from standard numerals to scientific notation and vice versa, in application problems.

5. Solve problems using elementary algebra. (CCC 2,7)
5.1 Define percent and utilize problem solving strategies to solve application problems involving percent.
5.2 Define and describe interest, principal, interest rate, simple interest, and compound interest , and use formulas to solve application problems.
5.3 Define and describe real numbers, irrational numbers, square root , radical sign , and radicands.
5.4 Use the Pythagorean Theorem, and properties of the Real Number System to solve application problems.
5.5 Define and describe the nth root , index, and the properties of radicals and rational exponents, and demonstrate their use by solving application problems.

6. Define basic geometric terms. (CCC 1,2)
6.1 Define the basic building blocks of geometry.
6.2 Define simple curves .

EVALUATION CRITERIA
Students will demonstrate proficiency on all Measurable Performance Objectives at least to the 75% level. The final grade will be determined using the College Grading System:

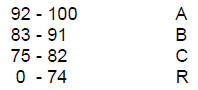
Students should refer to the Student Handbook for information on Academic Standing Policy, Academic Honesty Policy, Students Rights and Responsibilities and other policies relevant to their academic progress.