Arithmetic Operations in Bases Other Than Ten
The base-ten arithmetic algorithms discussed in the previous two sections
also work in other bases. In this section we apply the algorithms to base five.
Addition in Base Five
In base five the digits used are 0,1,2,3, and 4. Using blocks one can easily
build the following addition table.

All numerals in the table are written in base five with subscripts omitted.
Example 14.1
Compute 12five + 31five using blocks.
Solution .
Figure 14.1 shows how to compute 342five + 134five using
blocks.
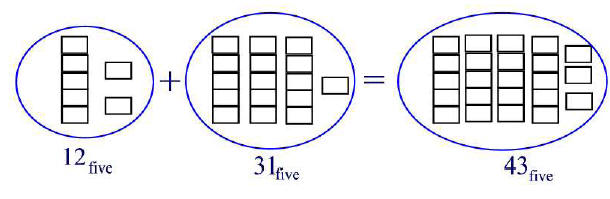
Figure 14.1
Example 14.2
Use a base five line to illustrate 12five + 20five:
Solution.
Note that 12five + 20five = 32five

Example 14.3
Compute the sum 342five + 134five
(a) using the lattice algorithm
(b) using the expanded algorithm
(c) using the standard algorithm.
Solution.

To check that the answer to the above addition is correct, we convert ev -
erything to base 10 where we feel comfortable.
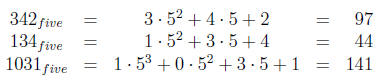
The result is confirmed since 97 + 44 = 141.
Practice Problems
Problem 14.1
Compute the sum 13five + 22five using
(a) base five blocks
(b) expanded algorithm
(c) lattice algorithm
(d) standard algorithm.
Problem 14.2
Perform the following computations.
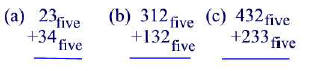
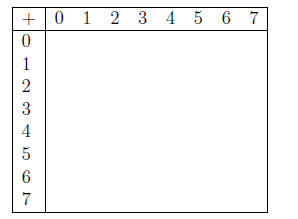
Problem 14.3
Complete the following base eight addition table.
Problem 14.4
Compute 132eight + 66eight:
Problem 14.5
Computers use base two since it contains two digits, 0 and 1, that correspond
to electronic switches in the computer being o or on. In this base, 101two =
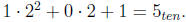
(a) Construct addition table for base two.
(b) Write 1101two in base ten.
(c) Write 123ten in base two.
(d) Compute 1011two + 111two:
Problem 14.6
For what base b would 32b + 25b = 57b?
Problem 14.7
(a) Construct an addition table for base four.
(b) Compute 231four + 121four
Problem 14.8
Use blocks to illustrate the sum 41six + 33six.
Problem 14.9
Use an expanded algorithm to compute 78nine + 65nine.
Problem 14.10
Create a base seven number line and illustrate the sum 13seven
+ 5seven
Problem 14.11
Construct an addition table in base seven.
Problem 14.12
Use the lattice method to compute the following sums.
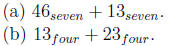
Subtraction in Base Five
The development of subtraction in base five from concrete to abstract is
shown in Figure 14.2.
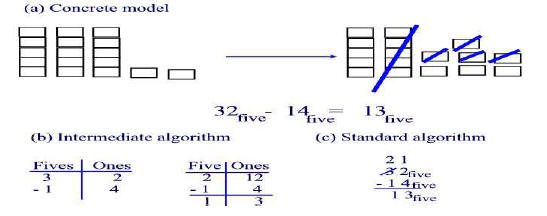
Figure 14.2
Example 14.4
Use base five number line to illustrate 32five-14five.
Solution.

Practice Problems
Problem 14.13
Perform the following subtractions:
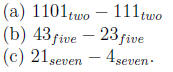
Problem 14.14
Fill in the missing numbers.
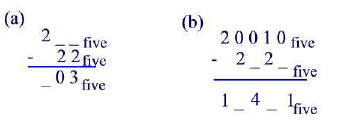
Problem 14.15
Use blocks for the appropriate base to illustrate the following problems.
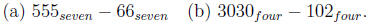
Problem 14.16
Use both the intermediate algorithm (discussed in Figure 14.2) and the standard
algorithm to solve the following differences.
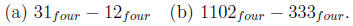
Problem 14.17
Use base five number line to illustrate the difference 12five-4five:
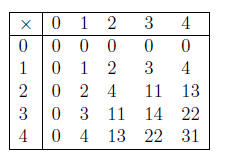
Multiplication in Base Five
Next, consider the multiplication algorithm. A base- five multiplication table
will be helpful.
Example 14.5
Calculate 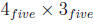 using base five number line.
using base five number line.
Solution.

So 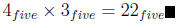
Example 14.6
Calculate 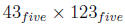 using
using
(a) the lattice method for multiplication
(b) the expanded algorithm
(c) the standard algorithm.
Solution.

Practice Problems
Problem 14.18
Create a base seven number line to illustrate 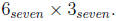
Problem 14.19
Find the following products using the lattice method, the expanded algo-
rithm, and the standard algorithm.
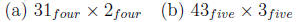
Division in Base Five
Long division in base five can be done with a long division analogous to the
base ten algorithm. The ideas behind the algorithms for division can be
developed by using repeated subtraction. For example,
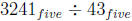 is
is
computed by means of repeated-subtraction technique as shown in Figure
14.3(a) and by means of the conventional algorithm shown in Figure 14.3(b).
Thus, 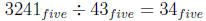 with remainder
with remainder
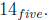

Figure 14.3
Practice Problems
Problem 14.20
Perform the following divisions:
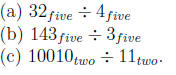
Problem 14.21
For what possible bases are each of the following computations correct?

Problem 14.22
(a) Compute 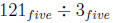 with repeated subtraction
algorithm.
with repeated subtraction
algorithm.
(b) Compute 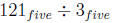 with long division algorithm.
with long division algorithm.
Problem 14.23
(a) Compute 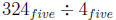 with repeated subtraction
algorithm.
with repeated subtraction
algorithm.
(b) Compute  with long division algorithm.
with long division algorithm.
Problem 14.24
(a) Compute  with repeated subtraction
algorithm.
with repeated subtraction
algorithm.
(b) Compute  with long division algorithm.
with long division algorithm.
Problem 14.25
Solve the following problems using the missing- factor definition of division,
that is, 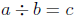 if and only if
if and only if
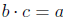 (Hint: Use a multiplication table for
(Hint: Use a multiplication table for
the appropriate base).
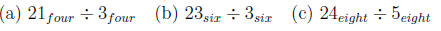
Problem 14.26
Sketch how to use base seven blocks to illustrate the operation

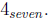
| Prev | Next |