Topics in Applied Mathematics

2 About the Course

Welcome to Applied Math 252b! This is a basic course for those who wish to learn about
the applications of mathematics in the real world . The main prerequisite is linear algebra
and calculus, and some familiarity with differential equations . While the course is primarily
for undergraduates, graduate students are also welcome. My hope is that the course will be
interesting and useful to students in a variety of fields and with a variety of backgrounds:
from physics to finance, economics to engineering, and math to biology

The official course description from the Yale Bulletin reads: “Topics in applied mathematics
including partial differential equations, optimization, variational calculus, and control.”
Since this is singularly unilluminating, here is a more detailed description.

The first major theme of the course is optimization, i.e., situations in which our goal is
to maximize or minimize some quantity subject to some laws that govern that quantity. For
example, we may wish to maximize profit by finding the most efficient way for a firm to
transport goods; or we may wish to find the configuration of gas molecules in a room that
has minimum energy (the “equilibrium” configuration); or we may wish to find the model
that best fits certain observed data from any field of application (the problem of regression in
statistics). All of these problems are instances of “minimum principles”, and in most cases,
they reduce to solving linear equations of various kinds. We will spend a good amount of
time in the course studying the common ideas underlying optimization problems from many
fields, and in particular, understanding why they give rise to linear equations .

The second major theme of the course is linear equations of various kinds:
• linear algebraic equations (hopefully you are already familiar with how to solve these)
• linear differential equations (hopefully you have seen these before)
• linear partial differential equations or PDE’s

While the motivation for studying many of these comes from optimization problems, the
tools used to analyze and solve them are completely different. The key idea is that of
diagonalization or eigenvalues, and we will use this idea to understand the following tools:

• The 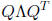decomposition of a symmetric matrix that leads to the solution of linear
differential equations.
• The Fourier transform or decomposition of a function into oscillations that leads to the
solution of many linear PDE’s.

As we study these analytical tools, we will also look at practical ways in which solutions can
be found using a computer. In particular, there will be a few computational problems in your
homeworks in addition to the “theory” problems.

A third important theme is the effect of nonlinearity, although we will only scratch the
surface of this difficult subject. Both for general nonlinear optimization and for nonlinear
differential equations, practical numerical methods are often as important as the theory, and
this will be reflected in the way we study them.

In addition to these major themes, we may also explore several fun “extra” topics. Possibilities
include:

• Nonlinear dynamics and chaos.
• An analysis of different voting methods in elections, which turns out to be closely related
to many other phenomena.
• Dynamics of random systems , i.e., how do we study systems whose “differential equations”
have some randomness in them?

Due to time limitations, we will have to leave out at least some of these topics, but I will
make every effort to cover those topics that are of special interest to students in the class.