Division Algorithm , Euclidean Algorithm, Linear Diophantine Equations and Introduction to Modular Arithmetic

Introduction and Goals. How can one natural number be expressed as the product of
smaller natural numbers? This innocent sounding question leads to a vast field of interconnections
among the natural numbers that mathematicians have been exploring for literally
thousands of years. The adventure begins by recalling the arithmetic from our youth and
looking at it afresh. In this section we will explore the Division Algorithm , greatest common
divisors, the Euclidean Algorithm, and some consequences of these to finding integer
solutions to linear equations . We will develop skills in proving theorems by induction and
other means.

Many experiences in everyday life are cyclical—hours in the day, days in a week, motions
of the planets. This concept of cyclicity gives rise to the idea of modular arithmetic, which
develops the notion of numbers on a cycle. In this section, we will introduce the basic idea
of modular arithmetic, which we will develop further in future sections.

Definitions.

1. The natural numbers are the numbers {1, 2, 3, 4, . . .}.

2. The integers are {. . . − 3,−2,−1, 0, 1, 2, 3, . . .}.

3. Suppose a and d are integers, then d divides a, denoted d|a, if and only if there is
an integer k such that a = kd.

4. Suppose that a, b, and n are integers, n > 0. We say that a and b are congruent
modulo n if and only if n|(a − b). We denote this relationship as

a ≡ b (mod n)

and read these symbols as “a is congruent to b (mod n).”

We begin now with the first set of questions. “Theorem” denotes a mathematical
statement to be proved by you. For example,

Example Theorem. 3| − 9.

Then you would supply the proof, write it up clearly, and be prepared to present your
proof at the board. Your write-up might look like this :

Example Theorem. 3| − 9.

Example Proof. By definition, 3| − 9 means that there exists an integer k such that
−9 = 3k. So to prove that this definition is satisfied, we need to find an integer k such that
−9 = 3k. Since −9 = 3 · (−3), the definition is satisfied, so 3| − 9 is true.

Example Theorem. 3 ≡ 7 (mod 2).

Example Proof. −4 = 2(−2). So, by definition, 2| − 4. So 2|(3 − 7). But 2|(3 − 7) is
the definition of 3 ≡ 7 (mod 2), so the theorem is proved.

Note: In giving proofs, rely on the definitions of terms and symbols , and feel free to use
results that you have previously proved. Avoid using statements that you ‘know,’ but which
we have not yet proved.

1.1. Theorem. Let a, b, and c be integers. If a|b and a|c, then a|(b + c).

1.2. Theorem. Let a, b, and c be integers. If a|b and a|c, then a|(b − c).

1.3. Theorem. Let a, b, and c be integers. If a|b and a|c, then a|bc.

1.4. Question. Can you weaken the hypothesis of the previous theorem and still prove
the theorem? Can you replace the conclusion by 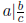and still prove the theorem?

1.5. Formulate your own theorem along the lines of the above theorems and prove it.

1.6. Theorem. Let a, b, and c be integers. If a|b, then a|bc.

1.7. Examples. Prove your answers. Is 45 ≡ 9 (mod 4)? Is 37 ≡ 2 (mod 5)? Is 37 ≡ 3
(mod 5)? Is 31 ≡ −3 (mod 5)?

1.8. Exercise. For each of the following congruences, characterize all the numbers m
that satisfy that congruence.

m ≡ 0 (mod 3),

m ≡ 1 (mod 3),

m ≡ 2 (mod 3),

m ≡ 3 (mod 3),

m ≡ 4 (mod 3).

1.9. Theorem. Let a and n be integers with n > 0. Then a ≡ a (mod n).

1.10. Theorem. Let a, b, and n be integers with n > 0. If a ≡ b (mod n), then b ≡ a
(mod n).

1.11. Theorem. Let a, b, c, and n be integers with n > 0. If a ≡ b (mod n) and b ≡ c
(mod n), then a ≡ c (mod n).

Note: If you are familiar with equivalence relations, you may note that the previous three
theorems establish that congruence modulo n defines an equivalence relation on the set of
integers. In the question before those theorems, 1.8, you described the equivalence classes
modulo 3.

1.12. Theorem. Let a, b, c, d, and n be integers with n > 0. If a ≡ b (mod n) and
c ≡ d (mod n), then a + c ≡ b + d (mod n).

1.13. Theorem. Let a, b, c, d, and n be integers with n > 0. If a ≡ b (mod n) and
c ≡ d (mod n), then a − c ≡ b − d (mod n).

1.14. Theorem. Let a, b, c, d, and n be integers with n > 0. If a ≡ b (mod n) and
c ≡ d (mod n), then ac ≡ bd (mod n).

1.15. Theorem. Let a, b, k, and n be integers with n > 0 and k > 0. If a ≡ b (mod n),
then a^k ≡ b^k (mod n).

1.16. Question. Illustrate each of the above theorems with an example using actual
numbers.

1.17. Theorem. Let a natural number n be expressed in base 10 as



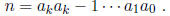
Then if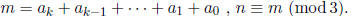

1.18. Theorem. A natural number that is expressed in base 10 is divisible by 3 if and
only if the sum of its digits is divisible by 3.

1.19. Question. Devise and prove other divisibility criteria similar to the preceding
one.

Well- Ordering Axion for the Natural Numbers. Let S be any non-empty set
of natural numbers, then S has a smallest element.

We will just assume that the Well- Ordering Axiom for the Natural Numbers is true. So
feel free to use it whenever you wish.

The Division Algorithm. Let n and m be natural numbers. Then (existence part)
there exist integers q (for quotient) and r (for remainder) such that

m = nq + r and

0 ≤ r ≤ n − 1 (r is greater than or equal to 0 but less than or equal to n − 1). Moreover,
(uniqueness part) if q, q' and r, r' are any integers that satisfy m = nq + r = nq' + r' with
0 ≤ r, r' ≤ n − 1, then q = q' and r = r'.