Experiment - Torsion of circular
Experiment - Torsion of circular rods
I. OBJECTIVES
1.1 To become familiar with torsion tests of rods with solid circular
cross sections.
1.2 To observe the relation between shear stress (τ) and shear strain (γ).
1.3 To experimentally determine the shear modulus (G) of three different
circular metal rods.
II. INTRODUCTION AND BACKGROUND
The stress distribution in a torsion member such as a transmission shaft is
non-uniform; it varies from zero at the centroidal longitudinal axis to a
maximum at the outer fibers.
In many engineering applications, such as torque transmission and in
springs, the torsional behavior critically governs the design. In many cases
the maximum torsional stress is the limiting factor in design while in
others, it may be the maximum permissible angle of twist.
III. EQUIPMENT
3.1 TERCO. Twist and Bend Machine, MT210.
3.2 3-8 mm diameter round rods of Steel, Aluminum, and Brass.
3.3 Tools: dial gauge, a micrometer, dead-weights, and other
miscellaneous equipment.
IV. PROCEDURE
4.1 Measure the actual diameters of the three rods, calculate the polar
moment of inertia of each rod and record the results on the data
sheet.
4.2 For a torque of 1.75 N-m (17.5 N at a radius of 100 mm), determine
the Factor of Safety with respect to yield for shear stress. The Factor
of Safety is the yield stress divided by the calculated stress.
Assume the following properties :
| Material | Shear Yield Stress (MN/m2) |
| Structural Steel (A36) | 145 |
| Aluminum Alloy (2024-T3) | 207 |
| Brass | 165 |
4.3 Check your results with the Laboratory Instructor before continuing
and obtain the rod gage length to be used in the tests.
4.4 Insert the first rod through the torsional fastening components of the
bearers and lock rod into the fixed bearer first. Adjust the distance
between the bearers to match the desired rod gauge length. The rod
should then be fastened into the free bearer with the lever close to
the upper limit pin.
NOTE: 5 to 10 in-lbs of torque on each Allen screw is sufficient to
lock each bearer. DO NOT OVER TORQUE THESE SCREWS.
Remember, the replacement cost of all damaged components will be
deducted from your laboratory fee refund.
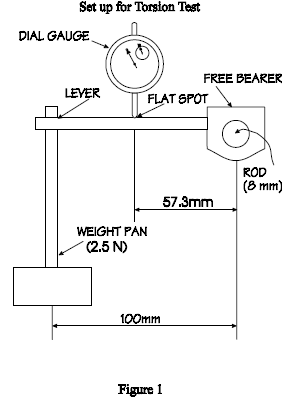
4.5 Locate the dial gauge support so that the gauge shaft is aligned with
the small groove at the center of the flat spot on the lever. Carefully
lower the gauge until the small hand reads 10. The large hand may
be set to zero by carefully rotating the outer ring of the dial face.
NOTE: The dimension between the groove on the lever and the axis
of the rod is 57.3 mm., thus, one revolution of the gauge corresponds
to one degree of twist in the rod.
4.6 Torque is applied to the rod by placing the knife
edges of the weight
pan in the groove near the tip of the lever. The weight of the pan is
2.5N. Adding three 5N weights produces the maximum allowable
torque. Before recording the lever deflections as a function of the
applied load, exercise the setup three or four times by applying and
removing the full 17.5N weight. This will allow minute slippages to
occur at the contact surfaces. You will be ready to record data when
the large hand of the dial gauge returns to the exact location (+ or -
1.0 unit) it was at prior to applying the load.
Apply torque to the rod in the increments indicated on the data sheet
and record the corresponding angle of twist. Record data during
both the loading and unloading cycle and note the amount of
hysterisis for each material.
4.7 Repeat steps 4.4 through 4.6 for the second and third rods.
V. REPORT
5.1 Make a plot of shear stress vs. shear strain for each rod. Each curve
should be approximately linear. Calculate the slope of the best
straight line fit through each set of data points. The slope of the
shear stress vs shear strain curve is the shear modules (G). using a
constant for each rod, derived from the following expressions :
τ = TR/J shear stress
γ = Rθ/L shear strain
G = τ / γ shear modulus
where:
T = torque applied to rod
R = radius of rod
J = Polar moment of inertia of rod (J= πr4/2)
L = gage length of rod
θ = maximum rotation of rod (radians)
A linear regression analysis, using spreadsheet program or a hand
calculator, is an acceptable alternative to drawing a best fit curve through
the data points for each rod. The regression analysis will use a least
squares fit to find the slope and y- intercept of a line through each set of
data points. The slope is the shear modules G.
5.2 Also discuss the following:
a. The linearity of the data for each material.
b. The amount of hysterisis observed.
c. Compare the shear moduli obtained by this experiment with
values given in appendices of two Strength of Materials texts.
Some references are:
DATA SHEET #1 FOR EXPERIMENT #4
STUDENT NAME ________________________GROUP #_______________
INSTRUCTOR NAME ______________________DATE OF EXP.__________
TABLE 1 ROD DIMENSIONS AND MAXIMUM STRESS
| SPECIMEN | #1 | #2 | #3 |
| MATERIAL | |||
| DIAMETER (mm) | |||
| POLAR MOMENT OF INERTIA (J) mm4 |
|||
| MAX TORSIONAL STRESS | |||
| F.S. SHEAR YIELD |
TABLE 2 ROD TWIST vs APPLIED LOAD
| SPECIMEN | #1 | #2 | #3 |
| MATERIAL | |||
| LOAD | |||
| 0 | |||
| 2.5 | |||
| 7.5 | |||
| 12.5 | |||
| 17.5 | |||
| 12.5 | |||
| 7.5 | |||
| 2.5 | |||
| 0 |
TABLE 3
COMPARISON OF RESULTS WITH
VALUES FROM TWO TEXT BOOKS
| SPECIMEN | ROD 1 | ROD 2 | ROD 3 |
| MATERIAL | |||
| from Experiment (GN/m2) | |||
| G from referece text 1 _________________ (GN/m2) |
|||
| G from reference text 2 _________________ (GN/m2) |
|||
| Maximum % Deviation |
| Prev | Next |