Foundations of Computer Science Assignment #2
The goal of this homework is to improve your formal proof
techniques and give you more insights on the
issues of countability. The first exercise is solved for you as an example . Some
theorems might follow
directly from theorems that appear before them, in such case you just need to
write out what follows from
what.
Exercise 1:
Show that the epigraph is true in the mathematical sense, i.e. |N| = |N − {1}|
Proof:
Let X = |N−{1}|. We show that |X| = |N| by demonstraing a bijection between
these sets. Let f : X → N
be defined as follows: f(n) = n−1. We claim that f is bijective. First observe
that f is injective. Indeed, let
f(a) = f(b) for some a, b ∈ X. Then a−1 = b−1 and a = b. Note that f is
also surjective: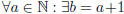 
such that f(b) = a and b ∈X. Indeed, f(b) = f(a + 1) = a + 1 − 1 = a; also
;
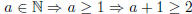hence a + 1 = b ∈ X.
Note: For any set X, if |X| = |N|, we are granted that a bijection Ø: N => X
exists. We can use Ø(n) to
obtain the element in X that corresponds to n, and use Ø-1(x) to get
the number that x corresponds to.
Observe that X was a subset of N, and since it didn’t include 1, it was a proper
subset. When can a
cardinality of a proper subset be the same as cardinality of its superset ? In
what cases does it happen ? We
shall explore it in the following Exercises. Bonus points will be awarded for
theorems labeled as ”Bonus”’.
First, prove what is almost clear from Exercise 1:
Proposition 1.1
|N| = |N − A|, where A = {1, 2, 3, ..., k}
Now let’s explore what happens if you take an infinite number of elements out of
N. Let’s take out all the
odd numbers. Prove or disprove the following:
Proposition 1.2
The even positive integers have the same cardinality as the natural numbers.
If you thought that the previous proposition was true and proved it, you might
have asked yourself if it is
the case in general.
Bonus Theorem 1.3
Every subset of N is either finite or has the same cardinality as N.
Hint: Use the fact that any nonempty set of positive integers has a least
element . If X is a subset of N,
show that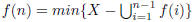 
gives the desired bijection for
infinite X.
What about supersets of N? After Exercise 1 it shouldn’t
be hard for you to prove that adding a finite
number of elements will not change the cardinality , but what if we double the
number of elements ? Prove
or disprove:
Exercise 1.4
|N| = |Z|.
The result of Exercise 1.4 can be generalized. Prove the following propositions:
Theorem 1.5
The union of two countable sets is countable.
Hint: Use the same technique as for Exercise 1.4; note to Exercise 1 might be
helpful. Consider finite and
infinte cases separately.
Theorem 1.6
Any subset of a countable set is countable.
Theorem 1.7
Intersection two countable sets is countable.
Theorem 1.8
Set difference two countable sets is countable.
Hint: Use Theorem 1.6
Now we can prove some interesting properties of infinite sets in general:
Theorem 1.9
Every infinite set has a countably infinite subset.
Hint: For a set X, look at the set Ø all injective maps from N into X. If Ø is
empty, then all the maps from
N to X are onto, and |N| ≥ |X|. You should be able to continue the proof
from here.
Bonus Theorem 1.10 (Dedekind’s Theorem)
A set is infinite if and only if there is a one-to-one function from the set
into a proper subset of itself.
Hint: If X be infinite and has a countable subset Y , let
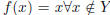. Complete the definition of f so
that f is a bijection between X and its proper subset. Write the proof in the
other direction to complete
the proof of the theorem.
Now we can move on to analyzing the first most interesting superset of N,
namely, Q. This set has a lot of
properties that make it substantially different from N . For instance, there is a
rational number between any
two rational numbers. Indeed, let a, c ∈ Q, then
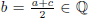and a ≤ b ≤ c. Also, any real
number can
be approximated with a rational number to an arbitrary degree: for instance,
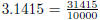is a rational
apporximation of π to within 10-4, but if we wanted a better
one, we could just continue writing out the
digits of π and get more and more precise approximations like 3.141592.
This cannot be done with integers,
which are a subset of Q. Now one might think that |Q| > |N| and, surprisingly,
be wrong, as we shall
demonstrate in what follows.
Theorem 1.11
|N| ≤|Q| ≤|N × N|
Hint: recall that |A| ≤|B| iff there is Ø: A => B which is injective,
and |A| ≥|B| if there is Ø: A=> B
surjective. Recall what it means for a number x to be rational.
Theorem 1.12
Union of countably many countable sets is of the same cardinality as N × N
Hint: lay out the sets in the union on a lattice grid, N × N.
Theorem 1.13, an important one
N × N is countable
Hint: look at the lattice grid. Start at the origin and try walking the grid in
such a way that any point in
it will be reached after a finite number of steps. One example of such walk
would be drawing Z × Z and
walking it in a spiral starting from the origin (see Figure 1); try to come up
with other kinds of walks. Then
the walk will be an enumeration of the points in N×N, since it yields a
bijection Ø(n) =(the point you reach
after n steps)
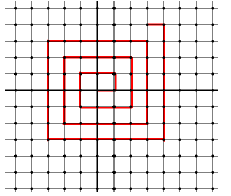
Figure 1: Lattice Walk on Z × Z
Corollary 1.14
Q is countable.
Corollary 1.14
Union of countably many countable sets is countable.
Corollary 1.14
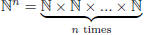is countable.
Now that we have seen that Q is countable, the question to solve would be
whether R is countable or not.
We shall approach this question slowly, first going back to subsets of N and
seeing how they realate to R.
Theorem 1.15
The set of all finite subsets of a countable set is countable.
Hint: make a list of such subsets; look at how many subsets there are of a
certain fixed size.
Theorem 1.16
For any set A, there is a one-one function f from A into P(A).
Theorem 1.17 (Cantor)
There is no function from a set A onto P(A).
Hint: look at some function Ø: A => P(A). Now for
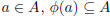(why?). So for each element of A we
have two cases:
1. 
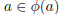. Call such elements
blue.
2. 
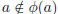. Call such elements red.
Look at the set of all red elements to obtain a contradiction.
Cantors Theorem implies that P(N) is not a countable set. A set that is not
countable is called uncountable.
So P(N) is an uncountable set. In fact, Cantors theorem implies that there are
infinitely many different
infinite cardinal numbers:
Corollary 1.17
There are infinitely many different infinite cardinalities.
Now we know that there’s an infinity of an order higher than that of the natural
numbers. Is R a set whose
order is of that kind ? Is R related to P(N) ? We shall answer these questions
in the following theorems.
Theorem 1.18
For a set A, let P be the set of all functions from A to the two point set 0, 1.
Then |P| = |P(A)|.
Hint: Each element in P(A) can be looked at as a function that tells whether an
element of A is in the
subset or not.
Theorem 1.19
Show that if A is finite, then |P(A)| = 2|A|
Hint: : use Theorem 1.18 to count all elements of P(A).
Corollary 1.20
There is a one-one correspondence between P(N) and infinite sequences of 0s and
1s.
Theorem 1.21
Let I = |[0, 1)|. Then |I| = |P(N)|.
Hint: write each number as infinite decimal.
Theorem 1.22
|R| = |[0, 1)|
Hint: you need to find a bijection between R and [0, 1). Perhaps the simplest
one can be represented
geometrically (see Figure 2)
Figure 2: Each point on the vertical segment corresponds
to a point on a line
Even though such demonstration by picture would be enough in most cases, you
should understand the
algebra behind it. Can you figure out the algebraic function f : [0, 1) ) =>
R represented on the picture ? You
can come up with your own bijection.
Now the time has come to combine the results of the theorems we’ve proven.
Theorem 1.23
R| = |P(N)| > |N|
At last, we’ve seen that there are more real numbers than natural numbers. To be
more specific, we
introduce the following notation: for a set A, 2A denotes P(A);
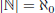(read: aleph null, from the name of
the hebrew letter aleph),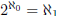 
, and in general
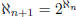. Then 
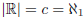. Now
one might wonder
whether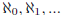 
represent all possible cardinalities
of infinte sets. In fact, all the common sets of numbers
we use: N,Z,Q,R,C are eithe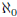r 
or
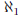. Is there a set with cardinality between
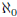and 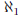? Can
we have
a set with cardinality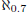 
or
?
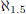This question has bothered the minds of mathematicians for many years, and the
proposition that there
is no set with cardinality between 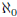and
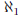is known as the Continuum Hypothesis,
conceived by Georg
Cantor (he was also the one who proved all the theorems above and invented the
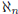notation). Now how
would one prove or disprove the hypothesis ? The answer is not simple. Here’s an
excerpt from Wikipedia:
”Cantor believed the continuum hypothesis to be true and tried for many years to
prove it, in vain. It
became the first on David Hilbert’s list of important open questions that was
presented at the International
Mathematical Congress in the year 1900 in Paris.
Kurt Godel showed in 1940 that the continuum hypothesis (CH for short) cannot be
disproved from the
standard Zermelo-Fraenkel set theory, even if the axiom of choice is adopted.
Paul Cohen showed in 1963
that CH cannot be proven from those same axioms either. Hence, CH is independent
of ZFC. Both of these
results assume that the Zermelo-Fraenkel axioms themselves do not contain a
contradiction; this assumption
is widely believed to be true.”
So we can either safely assume existence or nonexistence of sets with
cardinalities between aleph0 and aleph1
without ruining the basis on which current mathematics stands on. You are free
to make your choice on the
truth of the hypothesis.
Thus we finish our list of theorems to prove and turn to some problems.
Problem 2.1
Bob and joe are playing the following game: Joe secretly writes down a sentence,
and Bob tries to read
Joe’s mind by telling precisely what Joe has written. Joe is a kind person, so
he allows Bob to make infinite
number of mistakes, and the sentence stays the same after each try. If Bob get
the sentence correctly, Bob
wins. Is there an optimal strategy for Bob ? Is there an optimal strategy for
Joe ?
Problem 2.2
Bob and Joe are playing another game. Bob thinks of a real number, and Joe tries
to guess it. Bob remembers
how kind Joe was, and allows for infinite number of mistakes. An eternity
passes, but Joe still can’t get the
number (why?), so Bob allows Joe to win even if he doesn’t get the answer
precisely. Now Joe has to guess
the number to within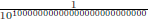 
. Can Joe win now ?
What if Bob thought of a point in Rn
and made Joe guess the location to that precision ?
Problem 2.3
Suppose a submarine is moving in a straight line at a constant speed in the
plane such that at each hour, the
submarine is at a lattice point. Suppose at each hour you can explode one depth
charge at a lattice point
that will kill the submarine if it is there. You do not know where the submarine
is nor do you know where
or when it started. Prove that you can explode depth charges in such a way that
you will be guaranteed to
eventually kill the submarine.
Geometrical Proof:
Let X be the set of points of a unit hemisphere, i.e X = {(x, y, z)|x2
+ y2 + z2 = 1 ^ z < 0}. Show that
|X| = |R2|.
Hint: raise the hemishpere 1 unit up, so it lies on the cartesian plane; then
the bijection is very similar the
one in Figure 2. If the proof seems hard, try showing a bijection between the
real number line and the set
of points belonging to a unit semicircle Y = {(x, y)|x2 + (y - 1)2
= 1 ^ y < 1}
Interesting Fact
Let X = [0, 1].Show that |X| = |X2|. Then show that |R| = |R2|.
Then show that |R| = |Rn| for any n ∈ N.
Hint: each element in [0, 1] can be written as a string 0.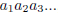
,
where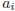 
∈ {0, 1, ..., 9} are decimal
digits .
Any element of [0, 1] × [0, 1] can be written as a pair of such strings. Find a
bijection between the set of
strings and the set of pairs of strings.
Interesting Corollary
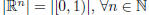
Fun Bonus Problem on Function Composition
Prove that using only one operation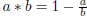 
, one can
get the sum , the product , the difference and the
ratio of any two numbers. You may use only the two numbers a, b that are
given and the operation *, i.e.
to use a number or an operation, you have to express it first in terms of a , b
and *.
So this is the end. Hopefully, you have enjoyed your homework !
| Prev | Next |