Fractions, Ratios, Money, Decimals and Percent
Lesson Five
| Purpose | Learn about equivalencies. |
| Summary | Students use paper folding and Power Blocks to
generate lists of equivalencies, which they then search for patterns. |
| Materials | Paper, Power Blocks, chalkboards. |
| Topic | Folding paper, recording the equivalencies formed. |
| Topic | Finding and recording Power Block equivalencies. |
| Homework | Paper folding can be shared at home. |
Painting the house...
Three parents chatting in the stands at their children's hockey game:
First parent: The older my kids get, the harder it is for me to help them
with their homework.
Did you ever figure out the house-painting problem they brought home last night?
Second parent: I hate problems like that . I tried to think of all the algebra I
could remember, but
I didn't have a clue which numbers to put in which equations .
Third parent: What was the problem?
Second parent: One man can paint a house in three hours. A second man takes five
hours to paint
the same house. How many hours will it take both men to paint the house
together?
Third parent: Well, you know it will take both the men less than three hours.
First parent: Why do you know that?
Third parent: Because if the first man can paint the house in three hours, it
isn't going to take
him as long to paint it with the other guy's help.
Second parent: How would you set the problem up to solve it in algebra?
Third parent: Well, how long does it take the first man to paint the house?
Second parent: Three hours.
Third parent. If it takes him three hours to paint the whole house, what
fraction of the house
would the man have painted in an hour?
First parent: A third?
Third parent: Right. He paints a third of the house in an hour. How much of the
house does the
second man paint in an hour if he takes five hours to paint the whole house?
Second parent: A fifth?
Third parent: So, the first man paints a third of the house in an hour, and the
second man paints a
fifth of the house in an hour. Working together, how much of the house would the
two of
them paint in just one hour?
First parent: A third plus a fifth?
Third parent: What's a third plus a fifth?
Second parent: Okay, we can't add a third to a fifth. We have to change both
fractions to
fifteenths. A third is 5/15 and a fifth is 3/15.
First parent: Why fifteenths? You lost me.
Third parent: We need a common denominator before we can add a third to a fifth.
Fifteenths is
the first fraction that a fifth and a third are equivalent to . What's 3/15 plus
5/15?
First parent: Eight fifteenths. But how do you know that it is 3/15 and 5/15?
Third parent: Oh, that's just the pattern for equivalencies. You multiply the
two denominators
together to get a common denominator. Then you multiply the numerators by the
same number
that you used to multiply the denominators. Since the numerators we started with
were ones,
the new numerators are just the numbers three and five, respectively.
First parent: Whatever.
Third parent. So, in the first hour they paint eight-fifteenths of the house.
How much would
they paint in two hours?
Second parent: Eight-fifteenth plus eight-fifteenths is sixteen-fifteenths.
Third parent. Sixteen-fifteenths is one fifteenth more than they need to do.
Once they have
painted the whole house, they stop.
Second parent: So it takes them an hour and seven-fifteenths to paint the house.
First parent: But where's the algebra?
Third parent: Why use algebra? All you need to know is fractions and
equivalencies.
Equivalencies...
Teacher: What is the answer to this problem?
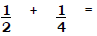
Would our students know that the answer to this problem is
3/4 and not 2/6? The fractions in our
students' lives come from sharing cookies, cutting cake, or dividing up marbles.
Do our students ever
use equivalencies?
If we meet in half an hour, is it the same if we meet in thirty minutes instead?
Equivalencies are as
common as the time of day. A half dollar and a quarter are 50¢ (or 50/100) and
25¢ (or 25/100),
respectively. We use equivalencies to add the half and the quarter together to
find their sum .
Equivalencies are as common as the coins we carry in our purse or pocket.
Equivalencies are a daily
part of life.
One is what we say it is...
For the Power Blocks in Lesson One, our students learned that one is what we say
it is. The S-1 square
could as well be one as T-1 or S-5. For the people fractions of Lesson Three,
our students also learned
that one is what we say it is. One row, one class, one family.
Teacher: Take a single piece of paper and fold it carefully down the middle.
(illustration 11-5-1)
(Single piece of paper and the same piece of paper folded in half.)
Teacher: How many pieces of paper did I say for you to take?
Students: One.
Teacher: What do we call the pieces that we get from our careful fold?
Students: Halves.
If our students do not know the words we expect them to say, we teach the
vocabulary.
Teacher: Please show me on your individual chalkboards how you would write a
half.
Students: 1/2
Teacher: Fold your paper carefully in half again like this.
(illustration 11-5-2)
(Show the sheet folded into fourths.)
Teacher: Now, what do we call the pieces that we get
from our second fold?
Students: Fourths.
We may teach our students to say fourths. We may also teach our students to say
one over four.
Teacher: Please show me on your individual chalkboards how you would write a
fourth.
Students: 1/4
Teacher: Fold your paper carefully in half again.
(illustration 11-5-3)
(Show the sheet folded into eighths.)
Teacher: What do we call the pieces that we get from this fold?
Students: Eighths.
Teacher: Please show me on your individual chalkboards how you would write an
eighth.
Students: 1/8
Teacher: Fold your paper carefully in half again.
(illustration 11-5-4)
(Show the sheet folded into sixteenths.)
Teacher: Let's record what we have found so far. How many pages did we each
start with?
Students: One.
1
Teacher: How many halves did we get from our first fold?
Students: Two.
Teacher: How would you write two halves?
Students: 2/2.
If our students do not know, we show them what two halves look like written out.
1 = 2/2
Teacher: How many fourths did we get from our second fold?
Students: Four.
Teacher: Show me how to write four fourths.
Students: 4/4.
1 = 2/2 = 4/4
The questioning continues. The writing continues, as well.
1 = 2/2 = 4/4 = 8/8 = 16/16
Teacher: Show me on your chalkboards how many fourths there are on one-half
of your paper?
Students: 2/4
1/2 = 2/4
Teacher: How many eighths?
Students: 4/8
1/2 = 2/4 = 4/8
Teacher: What question am I going to ask next?
Student: How many sixteenths.
1/2 = 2/4 = 4/8 = 8/16
Teacher: How many eighths in a fourth?
1/4 = 2/8 = 4/16
Teacher: Look at the numerators and the denominators of
all these fractions and see what
patterns you can find. Share with the rest of us any patterns that you see.
Paper can be folded more ways than in half and half again.
Teacher: Let's try folding a piece of paper in a different way to see what we
can see. The rule for
folding is that each new fold we make must divide the paper equally. As we fold,
we'll
record the fractions that we find.
(illustration 11-5-5)
(Paper folded in thirds, then in half then in thirds again.)
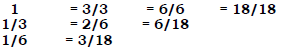
Teacher: What happens to the size of the denominator as
the number of folds increases? Are
there patterns that you can see? Can you use the patterns to help you predict
what the
numbers will be before you fold the paper to find out?
Once the students understand paper folding, they fold new pieces and keep track
of the fractions that
their folds produce.
Some fractions have the same value as other fractions, some do not: 1/3 is
equivalent to 2/6, but 1/3
is not equivalent to 1/2. What makes some fractions equivalent to others and
some not are rules to be
discovered and patterns to be seen.
See it once, see it again...
Teacher: The S-5 square is one . Make S-5 with two pieces that are equal in size.
(illustration 11-5-6)
(S-5 with two T-5 blocks alongside made into the S-5 shape and two R-4
rectangles also made into the
S-5 shape.)
Teacher: I'm going to keep a written record of what we find.
1 = 2/2
Leave the halves that you have found next to your S-5 shape. Is there any way to
divide the S-5
square into thirds? Remember, all the pieces have to be the same size or the
same area.
Students: (After trying for awhile) No.
Teacher: Is there any way to divide the S-5 square into fourths?
Students: Yes.
Teacher: Show me all the ways that you can find.
(illustration 11-5-7)
(Show the T-4, T-8, R-2 and S-3 shapes as fourths, with the halves still
visible.)
Teacher: I'll add what you have found to my list.
1 = 2/2 = 4/4
1/2 = 2/4
| Prev | Next |