graph a linear function
Use the slope and y -intercept to graph the linear function .
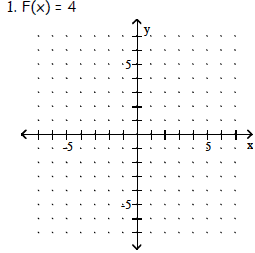
Objective: (2.1) Graph a Linear Function
Determine whether the given function is linear or nonlinear.
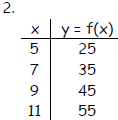
Objective: (2.1) Graph a Linear Function
Determine the average rate of change for the function .
3. F(x) = -9
Objective: (2.1) Use Average Rate of Change to Identify Linear Functions
Graph the function. State whether it is increasing, decreasing, or constant..
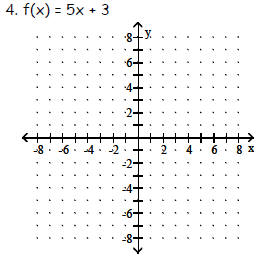
Objective: (2.1) Determine Whether a Linear Function is
Increasing, Decreasing, or Constant
Find the zero of the linear function.
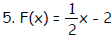
Objective: (2.1) Find the Zero of a Linear Function
Solve the problem .
6. A truck rental company rents a moving truck one day by charging $27 plus
$0.13 per mile. Write a linear
equation that relates the cost C, in dollars, of renting the truck to the number
x of miles driven. What
is the cost of renting the truck if the truck is driven 200 miles?
Objective: (2.1) Work with Applications of Linear Functions
7. Let f(x) be the function represented by the dashed line and g(x) be the
function represented by the
solid line. Solve the equation f(x) = g(x).
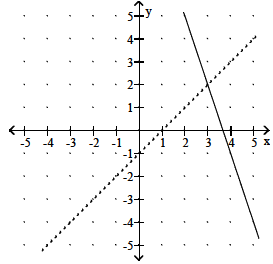
Objective: (2.1) Find the Zero of a Linear Function
8. Let f(x) be the function represented by the dashed line and g(x) be the
function represented by the
solid line. Solve the equation f(x) < g(x).
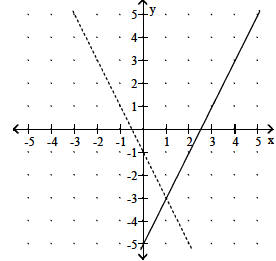
Objective: (2.1) Find the Zero of a Linear Function
If y varies directly as x, find a linear function which relates them.
9. y = 8 when x = 24
Objective: (2.2) Construct a Linear Model Using Direct Variation
Solve.
10. If the resistance in an electrical circuit is held constant, the amount of
current flowing through the
circuit varies directly with the amount of voltage applied to the circuit. When
5 volts are applied to a
circuit, 125 milliamperes of current flow through the circuit. Find the new
current if the voltage is
increased to 10 volts.
Objective: (2.2) Construct a Linear Model Using Direct Variation
Use factoring to find the zeros of the quadratic
function. List the x-intercepts of the graph of the function.
11. f(x) = x2 + 5x - 24
Objective: (2.3) Find the Zeros of a Quadratic Function by Factoring
12. G(x) = x2 + 5x
Objective: (2.3) Find the Zeros of a Quadratic Function by Factoring
13. f(x) = x2 - 81
Objective: (2.3) Find the Zeros of a Quadratic Function by Factoring
Find the zeros of the quadratic function using the Square
Root Method . List the x-intercepts of the graph of
the function.
14. g(x) = (x - 7)2- 4
Objective: (2.3) Find the Zeros of a Quadratic Function Using the Square Root
Method
Find the zeros of the quadratic function by completing the square. List the
x- intercepts of the graph of the
function.
15. F(x) = x2 + 14x + 13
Objective: (2.3) Find the Zeros of a Quadratic Function by Completing the Square
Find the real zeros, if any, of each quadratic function using the quadratic
formula . List the x-intercepts, if
any, of the graph of the function.
16. g(x) = x2 - 12 - 9x
Objective: (2.3) Find the Zeros of a Quadratic Function Using the Quadratic
Formula
Solve f(x) = g(x). Find the points of intersection of the graphs of the two
functions .
17. f(x) = 7x + 8
g(x) = x2
Objective: (2.3) Find the Point of Intersection of Two Functions
Find the real zeros of the function. List the x-intercepts
of the graph of the function.
18. F(x) = x4 - 26x2 + 25
Objective: (2.3) Solve Equations That Are Quadratic in Form
Graph the function f by starting with the graph of y = x2
and using transformations (shifting, compressing,
stretching, and/or reflection).
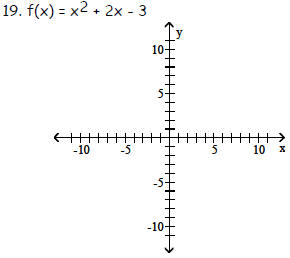
Objective: (2.4) Graph a Quadratic Function Using
Transformations
Find the vertex and axis of symmetry of the graph of the function.
20. f(x) = x2 + 2x - 3
Objective: (2.4) Identify the Vertex and Axis of Symmetry of a Quadratic
Function
Graph the function using its vertex, axis of symmetry, and intercepts.
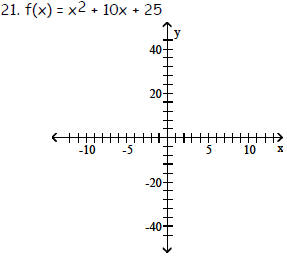
Objective: (2.4) Graph a Quadratic Function Using Its
Vertex, Axis and Intercepts
Determine, without graphing, whether the given quadratic function has a maximum
value or a minimum value and
then find that value.
22. f(x) = x2 - 2x - 5
Objective: (2.4) Find the Maximum or Minimum Value of a Quadratic Function
Solve the problem.
23. A projectile is thrown upward so that its distance above the ground after t
seconds is h = -13t2 + 468t.
After how many seconds does it reach its maximum height?
Objective: (2.6) Solve Applied Problems by Building Quadratic Functions
24. The owner of a video store has determined that the
cost C, in dollars, of operating the store is
approximately given by C(x) = 2x2 - 32x + 740, where x is the number of videos
rented daily. Find the
lowest cost to the nearest dollar.
Objective: (2.6) Solve Applied Problems by Building Quadratic Functions
Find the complex zeros of the quadratic function.
25. g(x) = 3x2 - x + 3
Objective: (2.7) Find the Complex Zeros of a Quadratic Function
Answer Key
Testname: 185 CH 2 REV FRA
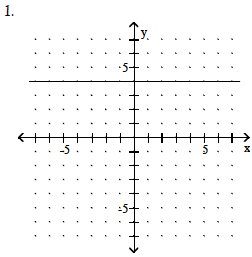
2. linear
3. 0
4. increasing
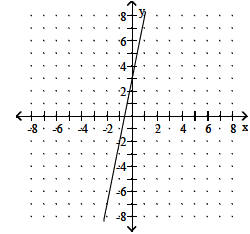
10. 250 milliamperes
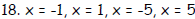
19
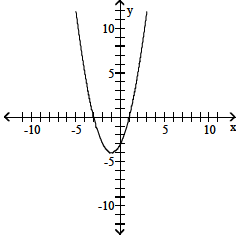
20. (-1, -4); x = -1
21. vertex (-5, 0)
intercepts (0, 25), (-5, 0)
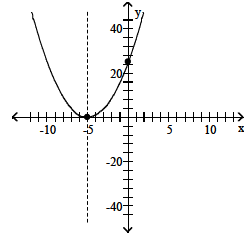
22. minimum; - 6
23. 18 s
24. $612
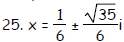
| Prev | Next |