Syllabus for College Algebra

Prerequisites: Two units of high school algebra and appropriate mathematics
placement result OR completion of Math 080.

Catalog Description: Functions (e.g., polynomial, exponential, and logarith-
mic). Zeros of polynomials . Solutions of systems of equations and in-
equalities. Triangle trigonometry . Selected topics from algebra such as
matrices and determinants, and the binomial theorem .

Objectives: After completing this course the student will be able to:

1. Determine the domain and codomain of relations and domain and
image set of functions.

2. Perform binary operations on functions .

3. Find the composite of two functions and determine its domain and
image set.

4. Determine if the inverse of a function exists and relate the graphs of
the function and its inverse.

5. Find the formula for the inverse of a one-to-one function.

6. Evaluate and graph functions including piece-wise defined functions.

7. Apply symmetries, reflections, and translations to curve-sketching.

8. Use technology to t curves to points in the xy-plane.

9. Solve exponential and logarithmic equations .

10. Apply exponential and logarithmic functions to solve real-world prob-
lems.

11. Apply polynomial and synthetic division to finding zeros of a poly-
nomial.

12. Apply the Remainder, Factor , and Rational Root Theorems to de-
termine zeros of a polynomial.

13. Sketch the graphs of polynomial functions.

14. Approximate zeros of polynomials.

15. Solve systems of equations and inequalities .

16. Evaluate and graph rational functions .

17. Graph a convex polygon to represent a given set of inequalities.

18. Determine the vertices of a convex polygon to maximize or minimize
a function of two variables .

19. Calculate the sum and product of two matrices when defined.

20. Perform scalar multiplication .

21. Apply the inverse of a (2 × 2 or 3 × 3) matrix to find the solution of
Ax = b.

22. Find a partial fraction decomposition for a rational function.

Text: Algebra & Trigonometry, Second Edition, John W. Coburn, McGraw-
Hill, ISBN: 007-808730-9
MathZone computer supplement is also required.

Material Covered: 2.4-2.8, Modeling with Technology 1, 1.4, 3.1-3.5, 4.1-4.5,
8.1-8.4, 9.1-9.4

Office Hours: Monday 9-10 A.M. and 2-4 P.M.
Tuesday 8-10 A.M.
Wednesday 9-10 A.M. and 2-3 P.M.
Thursday 8-11 A.M
Friday 9-10 A.M. Other times are available by appointment.

Calculator: A graphing calculator is required for this course. Any graphing
calculator is acceptable as long as it is not capable of symbolic computa-
tions like the TI -89 or TI-92. If you prefer to use a graphing calculator
that is not one of the TI series, I must approve it before you may use it
on tests.

Grading: There will be online homework assignments, 12 online quizzes worth
10 points each, and five tests worth 100 points during the course. Tests
will be given on September 25, October 16, November 6, and November
20, and December 9. There are NO make ups for tests. If you know ahead
of time that you will be missing a test, see me to arrange a time to take
it EARLIER. The final exam is scheduled for Wednesday, December 16,
from 5:15-7:15 P.M. The location will given at a later date. The final exam
cannot be taken at any other time. ALL graded work is to be done without
collaboration. You may not share a calculator with another person during
a test. The course grades will be computed as follows:

Five Tests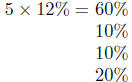
Quiz Total
Homework Total
Final Exam

The percentages translate into the grades as follows:

MathZone: There will be online homework assignments and quizzes that you
will be expected to do for this course. You will have as many tries as
you wish on each homework problem until you get it correct. Quizzes
will give you one attempt at each question. Homework assignments will
be available for 2 weeks after they are assigned or until the final exam
begins, whichever is soon. Quizzes will be assigned on Thursday nights
and will be available until 11:59 P.M. the following Tuesday. The Section
Enrollment Code is: EA8-8A-DAE.

Academic Accommodations: If you are eligible for academic accommoda-
tions due to a disability, please supply a letter from Student Academic
Support regarding the accommodations.

Attendance: Attendance is expected for all class meetings. In most cases, lack
of attendance leads to lower grades in the course.

Extra Help: If you need any help outside of class, feel free to drop by my office
to see if I am available. There is also a math lab where you may seek extra
help. It is open from 9 A.M. to 3 P.M. MTWR in HUB103A and from 4
P.M. to 9 P.M. MTWR in HU408.