Graphical Representations of Systems of Linear Equations

One of the great advantages of teaching with the computer is the quick and easy
access to the graphical representations of algebraic equations . In many situations, the
graph offers much more insight into the problem than does the algebra. This module
concerns a group of problems for which the graphs offer not only the insight into the
solution, but pose the problems as well.

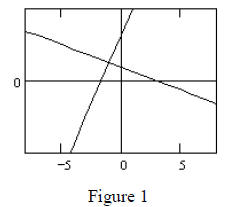
We will first consider a system of linear equations in general form, ax + by = c ,
where a, b, and c are in arithmetic progression . One example is 2x + 4y = 6 . Another is
3x - y = - 5. If we graph these two equations (Figure 1), it is not surprising that they
intersect, since the slopes of the lines are different .



If we now add to the system several more equations, as indicated in Figure 2, we
quickly see that something special, possibly surprising, is happening; something that is not
obvious from looking at the equations.

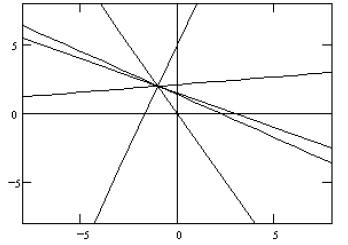
Figure 2

It is a simple task to solve the system to determine that the point (- 1, 2) lies on all linear
equations in general form whose coefficients form an arithmetic progression. Why should
this be so? If you consider the form of these equations, ax + (a + k) y = a + 2k , the
answer is clear. The right side of the equation has 2k, while the only term with k on the
left side is associated with y. For the two sides to be equal, y must equal 2. But if y = 2 ,
then on the left side we have ax + (a + k) 2= a + 2k , and x must equal - 1. The important
aspect of this problem is that the geometry of the system, not the algebra, was the
interesting and surprising part.

The next question to consider is, what happens if you try other patterns for a, b, and c?
Suppose we consider the system of linear equations in general form ax + by = c , where a,
b, and c form a geometric progression. What geometry does this system have? If you
begin by graphing equations of this form, there seem to be intersections all over the plane.

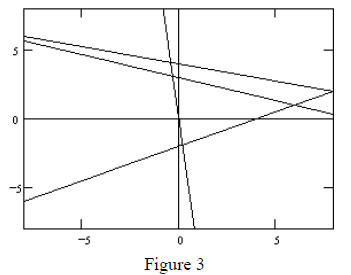
However, as more equations are graphed, something in the graph begins to take shape.


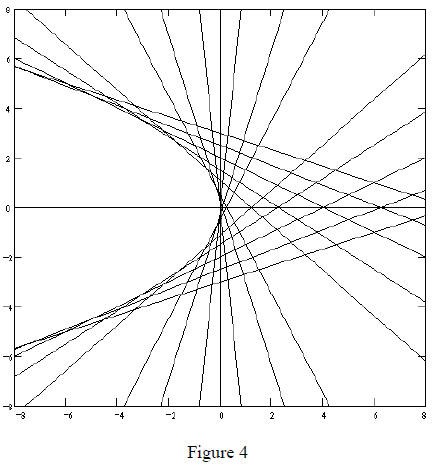
Notice that there is a region in the plane which has no intersections! What region
is this, and from where does it come? Solving the general system ax + ary = ar² and
bx + bsy = bs² gives solutions of x = - rs and y = r + s . How do these values of x and y
determine the "null" region in the plane? Students can play with the graph and guess the
boundary for the region. It appears to be a parabola of the form y² = - kx , for some
positive number k. Trying several values of k, students will quickly see that k = 4 gives a
good fit.

This boundary curve can be determined analytically by considering the equation
ax + ary = ar² as a quadratic function of r. Then r² - yr - x = 0 . Solving for r, we find
that 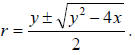Notice that no r exists for which y² - 4x < 0 . This means that no
linear equation of the form ax + ary = ar² passes through the region defined by y² < - 4x .

Notice that the two solutions x = - rs and y = r + s

satisfy this condition. That is, (r + s)² ≥-4(-rs) . To see this, combine all terms so that
r² + 2rs + s²- 4rs ≥ 0, and notice that the left side of the equation is a perfect square
r² -2rs+s ² = (r-s)²which is always greater than or equal to zero. The boundary for
the "null" region seen in Figure 4 is y² = - 4x . Again, there is nothing in the algebraic
representation of this system to indicate something quite spectacular is happening. Both
the problem and its solutions are motivated by the graphics.

Other similar questions naturally follow. Determine and explain the solution
patterns defined by considering the system ax + by = c , where a, b, and c are defined by:

1. a ×b = c , for differing values of c . eg. 2x + 5y = 10 , 3x - 4y = - 12 ,
and 6x + y = 6

2. fix c, ( c = 48 , for example) and a ×b = c . eg 4x + 12y = 48,
- 3x - 16y = 48 , and 12x + 4y = 48

3. a²  + b²  = c²

4.

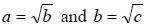
5. What figures are created if x is replaced by x²  in these equations?