Logarithms
For x > 0, a > 0, and a ≠ 1
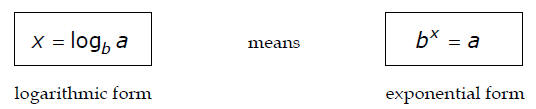
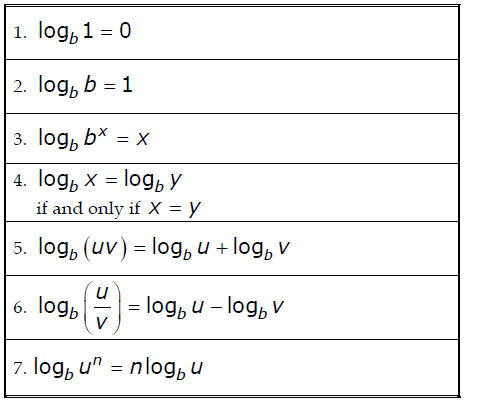
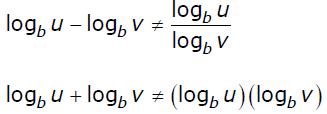
There is no formula to simplify these expressions:
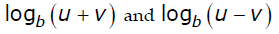
Solving Exponential Equations –
An exponential equation is an equation with the variable in an exponent.
1. Isolate the exponential expression (the base and exponent).
Ex: 100 ×1.023x = 200 Divide both sides by 100
1.023x = 2
2. Take the logarithm ( log or ln ) of both sides and bring
down the exponent using
property 7 on the other side of this page.
Ex: ln1.023x = ln2
3x ln1.02 = ln2
3. Solve for the variable and evaluate using a calculator
if necessary .
Ex:
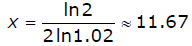
Solving Logarithmic Equations
1. Move all terms containing logarithms to one side of the
equation, and all other
terms to the other side of the equation.
Ex:
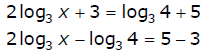
2. Combine the terms with logarithms to get a single
logarithm with a coefficient
of 1 using properties 5, 6, and 7 (work from the right side to the left of each
property).
Ex:
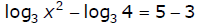Property 7
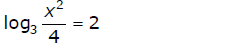Property 6
3. Rewrite the equation in exponential form.
Ex:
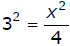
4. Solve for the variable and check all solutions in the
original equation.
Ex:
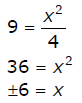
When checking, -6 does not give a solution since the
domain of all logarithmic
functions is x > 0. Therefore, the solution is x = 6.
NOTE: These procedures work for most equations, but
additional techniques such as
factoring may be required. Not all exponential and logarithmic equations are
possible
to solve.
| Prev | Next |