Get it on Google Play Get it on Apple Store

Math Final Exam Review Answer

1.2 Graph of Equation

1. Origin-Symmetry, y-axis symmetry, All (x,y and origin)-symmetry

2.(1) x-axis symmetry (2) y-axis symmetry (3) Origin symmetry

3.

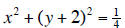
4. The center is the midpoint of (-4, -1) and (4, 1), which is (0,0)
And the radius is the distance b/w (-4, -1) and (0,0) or the distance b/w (4, 1) and (0,0).
Radius r is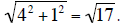 So the circle equation is x 2 + y2 =17.

5. center:(2, 3) and r = 4/3

6. center: (0,-1) and r =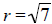

1.3 Linear equations in Two Variables

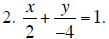  Multiplied by 4, the equation is - 2x + y = -4. so y = 2x - 4.

3. parallel line has same slope as 4x - 3y =7, that is m = 4/3.
So the line equation with m = 4/3 passing through (-3,2) is

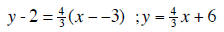
4. y = 1

5. The given equation solving for y is y = -6x +10.
So the perpendicular slope is 1/6.
Line equation with m=1/6 passing through (2, 5) is

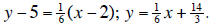
6. y = 7

7. (1) Two point from the given condition are (8, 0.21) and (15, 4.75).
m=0.65
y - 0.21 =0.65(t - 8);
y = 0.65t - 4.99

(2) In 2010, t =20. The cash flow per share is $8.01.

8. Two points (0,25000) and (10, 2000) So y = -2300x + 25,000

1.4 Function

1.
(a) Not a function
(b) Not a function
(c) Function
(d) Not a function
(e) Function
(f) Function

2.(1) Not a function (2) Function

3. (1) All real number (-∞,∞)
(2) Radicand ≥ 0; - x ≥ 0; x ≤ 0. So using interval notation (-∞, 0]
(3) Denominator ≠ 0; x2 + x -12 = 0; x = -4, 3; All real number but - 4, 3.
Using interval notation (-∞, - 4)∪(-4, 3)∪(3, ∞)

(4) 9x - 3 ≠ 0, at the same time 9x - 3 ≥ 0. So withouth equality sign , x > 1/3 .
Using interval notation (1/3 , ∞)

1.5 Analyzing Graphs of Functions


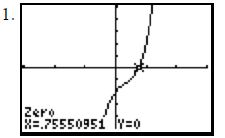
 No relative max and min value
There is one zero which is 0.75550951.

2. (1) Domain (-7, -∞) (2) Range [-6, -∞) (3) 4 zeros; x =1, 5.5, 8.5, 11.5
(4) Increasing (4, 6.5)∪(10,-∞ (5) Decreasing (-2, 4)∪(6.5, 10) (6) Constant (-7,-2)
(7) x - intercepts ; (1, 0), (5.5, 0), (8.5, 0), (11.5, 0) (8) y - intercept (0, 2)
(9) Relative max; 4 @x = 6.5 (10) Relative min; -6@x = 4 and -2@x =10

3. The average rate of change is

1.6 A library of Parent Functions

1.
(1) h(-2.3) = [[ 3(-2.3) – 1 ]] + 2 = [[ -6.9 – 1 ]] + 2 = [[ -7.9 ]] + 2 = -8 + 2 = -6.
(2) h(3.1) = [[ 3(3.1) - 1]] + 2 = [[ 9.3 – 1 ]] + 2 = [[ 8.3 ]] + 2 = 8 + 2 = 10.

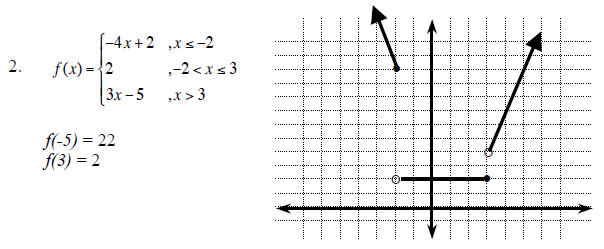
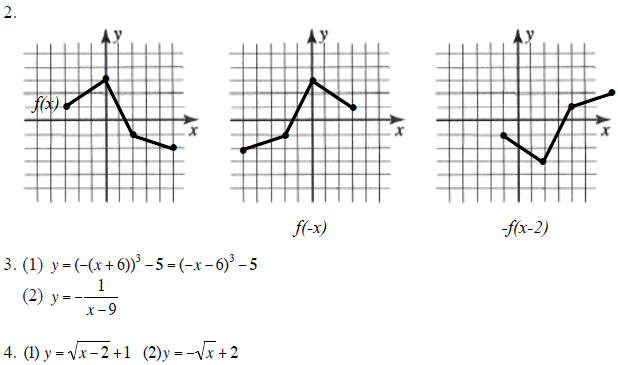
1.7 Transformation of Functions

1.(1) reflection across x-axis, 1 unit to the left and 4 units up
(2) 2 units up
(3) reflection across x-axis, 1 unit to the left and 8 units up

1.8 Composite function

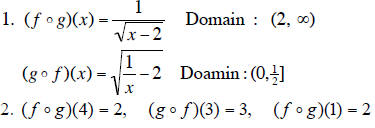
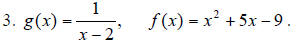
4. X( t ) = 50t (there is a typo in the problem for this part) and C( x ) = 60x + 750

(2) It's a Cost function depending on hours

1.9 Inverse Function

1.(1) Yes, b/c domain is restricted the graph shows only half of the function.
(2) No. Horizontal-line Test

2.

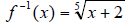
3. 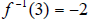f means f(-2) = 3. So 3 = k(2 - ( -2) - ( -2)3 )
3=12k, k=1/4.

4. You don’t even need to consider what the given function is.
It’s always true that

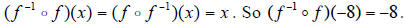
5. Switch x- coordinate and y -coordinate and connect the points. Your inverse graph
should be symmetry to y=x.

2.1 Quadratic function

1.(1) The vertex is (2,4) and it’s parabola open downward passing through (0,0).
So the equation is  y = -(x-2)2+4

(2) Vertex (1,-3), open upward, so y = a(x-1)2 - 3 Since it’s passing through (0,-2.5),
you can find “a”.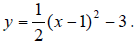

2.(1) ( ½ ,20) (2) x = ½ (3) No x-intercepts (4)(0,21) (5) all real number (6) [20,∞)
(7) ( ½ , ∞) (8) (-∞ , ½ ) (9) No max (10) 20 @ x = ½

3.(1) 1.5 (2) 104.01 ft (3) 228.64ft

2.2 Polynomial function with its graph

1(1) g(x) (2) h(x) (3) f(x)

2. Right-Hand: as x approaches ∞, y approaches -∞
Left -Hand: as x approaches -∞, y approaches ∞

3. (1) -(x+2)3 (x - 5)(x - 6)
(2) Odd multiplicity: crossing x- axis, starting from right lower corner .

2.3 Polynomial and Synthetic Division

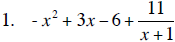
2. 245954
4. Yes. b/c the remainder using synthetic division is 0
5. False -4/7 is a zero.
6. Using synthetic division, remainder should be zero; your remainder should be c + 210.
So c + 210 = 0, c = -210

2.4 Complex number


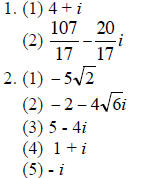
3. False

2.5 Zeros of Polynomial Function

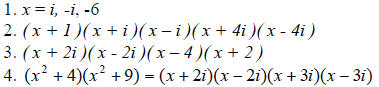
2.6 Rational Functions

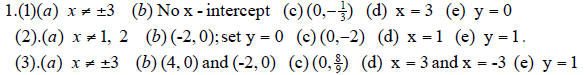
2.Domain is different. If you simplify
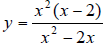then it is same as y = x .But
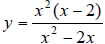is not defined at x = 0, 2 but y = x is.
The domain of 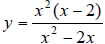is (-∞, 0)U(0, 2)U(2, ∞)
The domain of y = x is (-∞, ∞)

3.(1) g(x) = x +  5/x; VA: x = 0. Slant asymptote : y = x
(2) 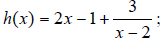  VA x=2 Slant asym: y = 2x- 1
The graphs are placed between two asymptotes. Check with your calculator

4.(1) substitute t =6 and 30 to get the corresponding N values’
(2) If you graph it, VA is x = -25 or t = -25 and HA is y = 1500 or N = 1500. So as
time increase, which means as t approaches ∞, N is approaching 1500. (Since it is
asymptote graph is not toughing or passing through).
So the limiting size is 1500.

2.7 Nonlinear Inequalities

1. Critical number is either undefined points or zeros. x = 0, 5

2. Put two functions into the calculator. One is
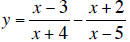and the other is y = 2.
Since we are looking for the intervals for
y ≤ 2, using intersection function key and
recognizing that VA’s are at x = -4 and x = 5, we will get the following interval as a
solution set .
(-∞, -8.7]U(-4, 2.7]U(5, ∞)

Prev Next