Polynomial Codes and some lore about Polynomials
10.4 Decoding a Single Error Correcting Code Generated by
a Primitive Polynomial
As outlined just above, to decode we first find the remainder of our received
message, r(x) upon dividing by the primitive polynomial p (x).
The obvious way to find this remainder is to divide and look at the remainder,
as
we have said. But there is an easier way which is based upon the fact that
the remainder
of a sum of polynomials is the sum of their remainders:
rem(a(x) + b(x)) = rem(a(x)) + rem(b(x)).
This means we can find the remainder of r(x) by summing up the remainders of
the
individual bits ( called monomials ) in it. This can be achieved very easily with
a
spreadsheet from the remainder table.
(You construct a second table whose rows are the entries of the remainder table
each
multiplied by the bit of r corresponding to that row. You then sum these
rows mod 2,
compute the binary number corresponding to that sum, and identify
the row of the
remainder table with that binary number. Switching that bit will
produce the sent
message, m(x)p(x).
Once you have found the remainder of the error and located it, can correct the
message to determine the sent message, you must then divide the sent message m(x)p(x)
by p(x) to find m(x). This can also be accomplished on a spreadsheet,
without a huge
amount of effort.
To do so, write the message to be divided from right to left as a column, (say
it is
0111001), and then write the code polynomial (say 1101) similarly from
right to left as a
column, to its left next to it. At each stage there are two
possibilities : either the top bit in
the previous column is 1 or 0 and your task
is to create the next column. If the top bit is 0
you shift the current column
upward by 1 into the next column; if the top bit is 1 you add
the code column
except for its top entry to the current column and shift up by 1 to create
the
next column. That is what long division does (looked at sideways)
Shifting the column over corresponds to looking at the next lower power . Adding
the code polynomial except for its top entry corresponds to replacing the
highest power in
the column by the corresponding lower powers of the code
polynomial, and entering the
fact that you have done so in the next column.
Here is what you get for the example given, when you divide the encoded
message
mp by the encoding polynomial p:
 |
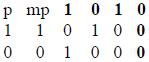= message |
| last entry is x2 term in remainder | |
| last entry is x term in remainder | |
 |
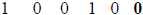last entry is constant term of remainder |
 |
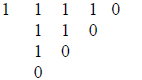What appears in the last column here is the remainder with
the most significant bit
at the top. Thus if the top bit were a, the next bit b,
and the bottom one c, this would
correspond to the remainder cba in our previous
notation, or c + bx + ax2, if our code was
defined by the polynomial 1 +x +x3.
Notice that you can get rid of the message part of the received word r(x) by
division as done here. I like the remainder table addition method for computing
remainders better than the long division method because the table has other
uses.
10.4 Comments
So far, we have introduced multiplication of polynomials as a way to code, and
seen a way to find and describe Hamming codes with k check bits using one
polynomial
of degree k, instead of filling in a 2k-k-1 by k matrix of check
bits.
The method of finding errors we have described here, by finding the remainder of
r(x) and discovering which power has that remainder, seems quite different from
the
method used for general matrix codes. That consisted of matrix multiplying
the
remainder r vector by the message killing D matrix and seeing what row of D
the answer
agreed with.
If we find the remainder by long division, the methods of error location seem
quite different.
However if you compute the remainder by adding up the remainders of the
powers
in r(x) you are actually matrix multiplying the r(x) row vector by the remainder
table matrix, and comparing the result with the rows of the remainder table
matrix. Since
the remainder table matrix when multiplied on the left by any code
word will give the 0
vector, the procedure from this point of view is identical
to the previous one. The
remainder table provides the message killing D matrix
for the code.
The code generated by a polynomial p can be considered a matrix code, in which
the first row contains the encoding polynomial written lowest power first
followed by a
string of 0's, and successive rows have that polynomial shifted by
1 to the right from their
immediate predecessors; in the final row the last
polynomial bit reaches the last column.
The remainders we encounter when dividing by a primitive polynomial can be
added
in the usual way. But if we have our remainder table, we can also multiply them.
Each non- zero remainder is remainder of a power of x,
which power can be
determined from the remainder table. We define the product of
two remainders to be
the remainder corresponding to the power that is the sum of
their powers. (when this
sum exceeds 2k-1 we can use the fact that x raised to
power 2k-1 is 1 to subtract 2k-1 from
that sum).
For example, with our old remainder table:
| Power |  |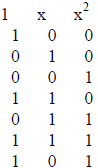
binary number |
 |
 |
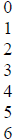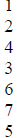we define the product of 110 and 111, which are the third
and fifth powers of x, to be x tp
the three plus five, or x8, which is x or 010.
The addition and multiplication defined here for a primitive polynomial
satisfy
all the standard laws that addition and multiplications of numbers obey; the
0
polynomial plays the role of 0, and the polynomial 1 plays the role of 1.
Obviously
the product of two powers is another power and that is never 0, and
the sum of two
remainders is another remainder.
Such remainders therefore form what mathematicians call a field, which implies
that they can be considered as number systems, like the real numbers or the
rational
numbers or the complex numbers or GF(2).
This is not true for remainders upon dividing by a factorable polynomial , like
p(x)q(x) with each factor of degree at least 1. The problem is that the
remainder of the
product of p(x) by q(x) is the 0 polynomial. This means that
two non-zero remainders can
have product 0. This is unacceptable for numbers
because it makes it impossible to find
inverses for such numbers.
A very important fact about real and complex numbers, which we want all
number
systems to preserve is: (It is a part of the fundamental theorem of algebra.)
A polynomial equation of degree k can have at most k solutions.
This statement is true if the coefficients of the polynomial are elements of a
field
and generally false otherwise.
This statement will be important to us so we now prove it.
Suppose we have a polynomial equation of degree k with
coefficients in a field.
If k is 1, the equation takes the form ax-b =0 for non-zero a. If c is a
solution we must
have ac=b which implies c = b/a, which tells us that c is
uniquely determined in a field
from a and b so long as a is not 0.
We suppose now that the statement (that an equation of given degree d has at
most d
solutions) is true for all polynomials of degree k-1, and prove that it
is true for any p(x) of
degree k.
Suppose c is a solution to the equation p(x)=0. Then (x-c) must divide p without
a
remainder. Otherwise we would have p(x) = (x-c)q(x) + r and p(c) = r and not
p(c)=0.
This means the we can write p(x) as (x-c) q(x), where q(x) has degree k-1 and q
has at
most k-1 solutions by our induction hypothesis.
Any solution to p(x) =0 therefore obeys (x-c)q(x)=0.
And we are done! x-c has only one solution and q(x), being of degree k-1, has at
most k-1
of them by the induction hypothesis.
Since no two non zero field elements have product 0, the only solutions to
p(x)=0 occur
where one or another of the factors of p is 0.
So p(x)=0 can have at most k solutions, as we set out to prove.
Now we ask: what can we possibly do to correct more errors in a polynomial
code?
Using a primitive polynomial, p(x) as encoding polynomial works splendidly to
correct one error, and we certainly want to maintain this power. To correct two
errors
we will use a polynomial that is the product of a primitive polynomial
and a second
polynomial which we choose to provide the additional information
that we need to
locate two errors.
What second polynomial do we choose here?
We will choose a polynomial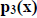 
which obeys the condition
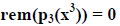
where we take the remainder on dividing by our primitive polynomial p as before.
And it will turn out that we can correct 3 errors by having a factor, p5 in the
encoding polynomial that obeys
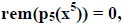
and so on, to correct more errors.
In the next chapter we address the two questions that arise here.
How do we find polynomials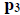 
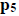and
and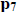 
and so on?
How can we locate and correct two or more errors if our encoding
polynomial has
such factors in it? Which will answer the question: Why do we want
such factors?
Codes of the form outlined here are called BCH codes, after the three people who
discovered them: Bose, Ray-Chaudhuri, and Hocquenam (do not count on the
accuracy of
my spelling.)
Exercises:1. Find all primitive polynomials of degree 6 (over the two element
field
GF(2) defined by 2=0.)
2. Pick a primitive polynomial of degree 5. Construct a spreadsheet encoder for
it,
that takes any binary message of length 26 and converts it into a coded
message
using that polynomial as encoding polynomial.
3. Construct a spreadsheet single error corrector for it, that starting with any
received message of length 31 takes its matrix product with the remainder table,
locates the error and corrects it.
4. Construct a spreadsheet divider that takes the corrected code word and finds
the
message that was encoded to it.
| Prev | Next |