Pre-Calculus Mathematics Test #1 Sample Solutions
1. Given are expressions involving intervals. For each
one, show an equivalent expression
involving inequalities.
(a) x is in
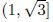
(b) x is in
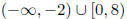
Solution:
(a)
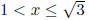
(b) x < −2 or 0 ≤ x < 8
2. Given are expressions involving inequalities. For each
one, show an equivalent expression
involving intervals.
(a) 0 ≤ x < 13
(b) x ≤ 0 or 3 < x < 4
(c) x ≠ 0
Solution:
(a) x is in [0, 13)
(b) x is in
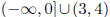
(c) x is in
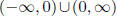
3. For each inequality, use interval notation to describe
the set of all x satisfying it.
(a) (x − 3)(x − 2)(x + 4) < 0
(b) |2x + 3| > 7
Solution to (a): The product (x−3)(x−2)(x+4) is
zero precisely when either x = 3, x = 2,
or x = −4, which leads us to consider the four intervals (−∞,−4), (−4, 2), (2,
3), and (3,∞)
(corresponding to the inequalities x < −4, −4 < x < 2, 2 < x < 3, and 3 < x,
respectively).
To determine the sign of the product in each of these
intervals, it suffices to determine the sign
of each factor in each interval and to apply the rule that the product is
negative if and only if
an odd number of its factors are negative.
This leads to the following table, which indicates the
sign of each factor (and, in the last line,
the sign of the product) within each interval.
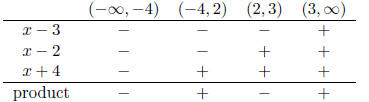
We see, then, that the product is negative when x is in
the set
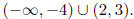
Solution to (b): To solve this, we recall that |a|
> b holds if and only if either a > b or
a < −b. (That is, a must be more than b units from zero, in either direction.)
Applying this principle, we get
2x + 3 < −7 or 2x + 3 > 7
2x < −10 or 2x > 4
x < −5 or x > 2
In interval notation, this translates into: x is in
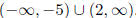
4. Describe (using interval notation or inequalities) the
domain of the given function. For a
small bonus, also describe its range.
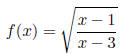
Solution: The expressions x − 1 and x − 3 are
defined everywhere, but their quotient is
undefined when x = 3. Hence, 3 is excluded from the domain. Because the square
root
operator is being applied to the aforementioned quotient, any value of x making
it negative is
also excluded from the domain.
Now, a quotient a/b is negative precisely when exactly one
among a or b is negative. Regarding
x − 1 and x − 3, the only values of x that make exactly one of them negative are
those in the
interval (1, 3). (For all such values of x, x − 1 is positive and x − 3 is
negative. Of course,
because x − 1 > x − 3 for all values of x, there is no way to make x − 1
negative and x − 3
positive.) Hence, all values in (1, 3) are excluded from the domain.
As there is no reason why any other value would be
excluded from the domain, we conclude
that it consists of all real numbers except for 3 and those in (1, 3). That
leaves us with
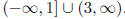
5. Consider the pair of points (−2, 5) and (2,−1).
(a) What is the length of the line segment connecting these two points ?
(b) What is the midpoint of the line segment connecting these two points?
(c) What is the slope- intercept equation of the line passing through these two points?
Solution:
(a) Recalling that the distance formula is
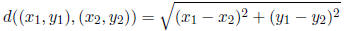
we calculate as follows:
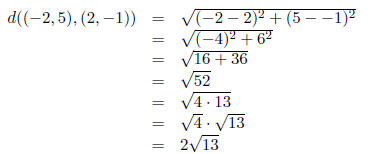
(b) Recalling that the midpoint of the line segment
connecting (x1, y1) and (x2, y2) is ((x1 +
x2)/2, (y1 + y2)/2), we calculate as follows:
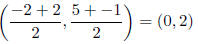
(c) Recall that the slope of the line passing through the points (x1, y1) and (x2, y2) is
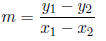
Applying that here, we get
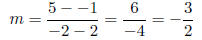
Now, starting with the point-slope equation, we derive the slope-intercept equation:
y − y1 = m(x − x1)
y − 5 = −3/2 (x − −2)
y − 5 = −3/2 (x + 2)
y − 5 = −3/2x − 3
y = −3/2x + 2
6. Consider the line described by the equation 2x + y + 4 = 0.
(a) Determine the slope-intercept equation of the line
that is perpendicular to it and that
passes through the point (3, 4).
(b) In the space below, sketch both lines (i.e., the given one and the one described in (a)).
Solution to (a): Recall that the line described by
Ax + By + C = 0
has slope −A/B (provided
B ≠ 0). Applying that here, the slope of the line given by 2x + y + 4 = 0 is −2.
Had we not
remembered this rule, we could have rewritten the equation as y = −2x − 4,
which, being in
slope-intercept form, tells us that the slope is −2.
The line we seek is perpendicular to that and hence has
slope 1/2 . (Recall that the product
of the slopes of two perpendicular lines (neither of which is vertical) is −1,
and here we have
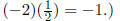
The line we seek also passes through (3, 4) Knowing its
slope and one of its points, we can start
with the point-slope equation and derive the slope-intercept equation:
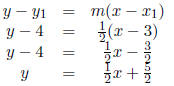
Solution to (b):
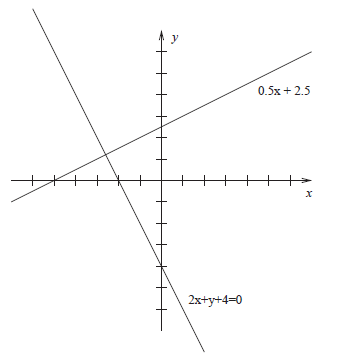
Figure 1: Answer for 6(b)
7. Consider the parabola described by the equation y = −x2 + 2x + 3.
(a) Determine the Vertex Form equation of this parabola.
(b) Sketch its graph in the space below.
(c) Determine the domain and range of the function described by this equation.
Solution to (a): Using the “complete the square” method:
y = −x2 + 2x + 3
= −(x2 − 2x) + 3
= −(x2 − 2x + 1 − 1) + 3
= −(x2 − 2x + 1) + 1 + 3
= −(x − 1)2 + 4
Solution to (b): From the answer to (a), we can
tell that the parabola’s vertex is at (1, 4)
and that it opens downward. For the purposes of drawing an accurate graph, it
would help to
know the x-intercepts. By factoring the given equation, we get
y = −x2 + 2x + 3 = −(x2 − 2x − 3) = −(x − 3)(x + 1)
which tells us that the x-intercepts are at 3 and -1.
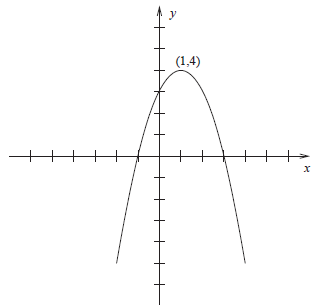
Figure 2: Answer for 7(b)
Solution to (c): The domain is all real numbers (i.e., (−∞,∞)) and the range is (−∞, 4].
8. Consider the circle described by the equation x2 + 6x + y2 − 2y − 6 = 0.
(a) Determine the standard form equation of this circle.
(b) Sketch its graph in the space below.
Solution to (a): Using the “complete the square” method:
x2 + 6x + y2 − 2y − 6 = 0
(x2 + 6x + 9) + (y2 − 2y + 1) − 6 = 0 + 9 + 1
(x + 3)2 + (y − 1)2 = 10 + 6
(x + 3)2 + (y − 1)2 = 16
Solution to (b): From the answer to (a), we can
tell that the circle’s center is (−3, 1) and
that its radius is
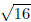 ,
or 4.
,
or 4.
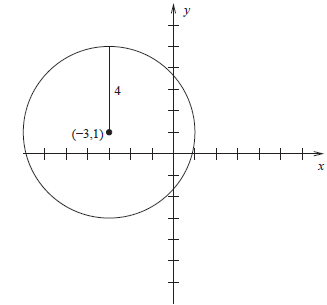
Figure 3: Answer for 8(b)
| Prev | Next |