Rational Expressions
• Rational Expression : A rational expression is the
quotient of two polynomials.
Example:
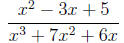
• Domain of An Algebraic Expression : The domain of
an algebraic expression is
the set of all numbers for which the expression is defined. (i.e. the set of all
numbers
that can be used in the expression without having a zero in a denominator or a
negative
number under an even radical)
Example: The domain of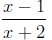 is all real numbers except -2. Since -2 would cause
is all real numbers except -2. Since -2 would cause
the denominator of this expression to be zero, we exclude it from the domain.
All other
real numbers may be substituted without any problems.
Example: The domain of
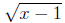 is all real numbers greater than or equal to
1. Since
is all real numbers greater than or equal to
1. Since
we cannot take the square root of a negative number, we need x-1 ≥ 0 which
implies
that x ≥ 1.
Example: The domain of
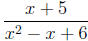 can be determined by finding the real numbers
can be determined by finding the real numbers
that will cause the denominator to be zero. Therefore, if we factor the
denominator it
will be clear what those numbers are: x^2 - x + 6 = (x - 3)(x + 2). We can see
then,
that 3 and -2 will cause the denominator to be zero. Hence, we exclude these
numbers
from the domain. The domain of the expression is all reals except 3,-2.
• Simplifying Rational Expressions: To simplify a
rational expression, follow these
steps:
1. Factor the numerator and denominator completely.
2. Cancel any factor that appears in both the numerator and the denominator.
Example:
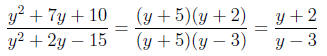
• Multiplying Rational Expressions: This is really
just an extension of simplifying.
The steps are as follows :
1. Factor the numerator and denominator of each rational
expression.
2. Cancel any factor that appears in a numerator and a denominator.
Example:
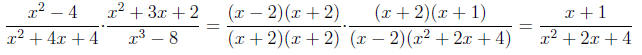
• Dividing Rational Expressions: After the first
step, follow the same strategy as in
multiplying rational expressions.
1. Invert (flip over) the rational expression you’re
dividing by (i.e. the second expression
or the one in the denominator of the large fraction )
2. Factor
3. Cancel
Example:
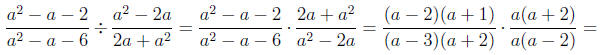
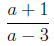
• Adding and Subtracting Rational Expressions:
Since rational expressions are
basically fractions, in order to be able to add them or subtract them, we must
first
have common denominators , and preferably the LEAST common denominator.
Strategy:
1. Factor the denominators.
2. The Least Common Denominator is the product of all the factors present raised
to the highest exponent that appears on the factor in the factorizations.
3. For each fraction, multiply the numerator and denominator by the factors that
are in the LCD , but not in the fraction’s denominator.
4. Add or subtract the numerators as appropriate to the problem.
5. Simplify.
Example:

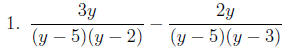
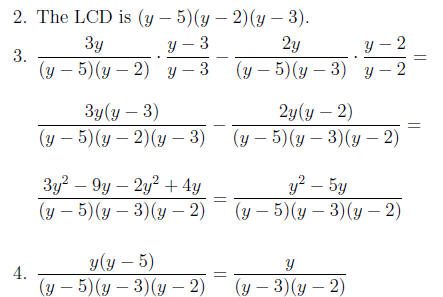
Try these: pp43-44: 4, 10, 16, 34
Answers:
4.) All reals except 1,-1,-2
10.) 1
16.) a - b
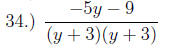
| Prev | Next |