Rational Number Project
| Fraction Operations and Initial Decimal Ideas Lesson 1: Overview |
Materials
• Fraction Circles for students • Student Pages A, B, C, D |
| Students review how to model
fractions with fraction circles by ordering unit fractions, using 1-half as a benchmark to order two fractions , and comparing fractions close to one. |
| Teaching Actions Warm Up Order these fractions from smallest to largest. Be
|
Comments Your
goal is to reinforce students’ Here is an example:
1/10 is farthest from the whole. Five |
| Large Group Introduction
1. Start the lesson by asking student to share their 2. Questions to guide discussion: • Which is bigger 3/4 or 3/5? • Which fraction is just under 1/2? • Which fractions are just greater than 1/2? • Which fractions are close to one whole? • Why is 1/10 the smallest? |
|
| 3. Spend some time ordering 3/4 and 14/15.
• Which fraction is closer to 1? How do you • One student suggested the two fractions are • Verify your conclusion by modeling each |
Expect some students to struggle with 3/4 and 14/15. Misunderstandings to expect are: • Equal, as both are one away • 3/4 is larger because the |
| 4. Test students understanding by asking them to
order 4/5 and 8/9. Which is closer to a whole? Verify students’ responses by showing both fractions with fraction circles.
|
Behind this strategy is the ability to mentally represent both fractions using images of fraction circles. Here is an example of a 6th grader’s use of mental images to order 8/9 and 4/5. 8/9 is larger because if you get the fraction circles out, 1/5 is bigger than 1/9. So if you put 8/9 and 4/5, 8/9 would be bigger because it would have smaller pieces so there is going to be a small amount left and it’s going to be a bigger piece left for 4/5. |
| 5. Summarize the main ideas from this lesson introduction: • You can judge the relative size of fractions by thinking about fraction circles. • Using 1/2 as a benchmark is helpful. • Thinking about how close a fraction is to one whole is also helpful when comparing fractions like 3/4 and 5/6 or 4/5 and 99/100. Small Group/Partner Work |
Notice how this student uses his ability to order two unit fractions (1/5 and 1/9) to answer this.
|
| 6. Student pages A-D reinforce comparing
fractions to 1/2, comparing fractions to unit fractions, and comparing fractions close to 1. |
|
| 7. Present this problem: What do you think of
this students’ reasoning? 6/8 is greater than
4/11 because with 6/8 you need 2 to get to |
This is a common error in student thinking. While the student gets a correct answer, her reasoning will not generalize to all fraction pairs. With fractions you have to consider the relative size of the amount away from one whole. |
8. Does this student’s strategy work for
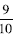 and and
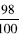 ? ? |
Possible explanations are as follows:
• Doubling the numerator gives • If the numerator is 7 then
|
| 9. To assess their understanding of using 1/2 as
a benchmark ask this question: • Juanita said
that • Will said he knew
• I understand Juanita’s strategy but I don’t |
Translations:
• Symbolic to Manipulative to Verbal;
• Symbolic to Verbal
Additional Notes to the Teacher
Lesson 1
The RNP level 1 lessons support students’ development of
informal ordering strategies. Four
informal ordering strategies have been identified: same numerator, same
denominator,
transitive, and residual. These strategies are not symbolic ones, but strategies
based on
students’ mental representations for fractions. These mental representations are
closely tied to
the fraction circle model.
Same denominator: When comparing
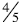 and
and 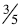 students can conclude that
students can conclude that 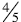 is larger
is larger
because when comparing parts of a whole that are the same size (in this case
 ) then 4 of those
) then 4 of those
parts are bigger than 3 of them.
Same numerator: When comparing
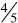 and
and 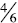 ,
students can conclude that
,
students can conclude that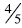 is bigger
because
is bigger
because
5ths are larger than 6ths and four of the larger pieces will be bigger than 4 of
the smaller pieces.
Students initially come this understanding by comparing unit fractions.
Transitive: When students use benchmark of ½ and
one they are using the transitive property.
When comparing 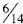 and
and
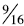 students can conclude that
students can conclude that
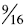 is larger because
is larger because
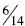 is a little less
is a little less
than ½ and 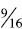 is a little more than ½.
is a little more than ½.
Residual: When comparing fractions
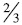 and
and 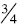 students can decide on the relative size of each
students can decide on the relative size of each
fraction by reflecting on the amount away from the whole. In this example,
students can
conclude that ¾ is larger because the amount away from a whole is less than the
amount away
from the whole for  . Notice that to use this
strategy students rely on the same numerator
. Notice that to use this
strategy students rely on the same numerator
strategy; they compare 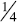 and
and
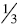 to determine which of the original fractions
have the largest
to determine which of the original fractions
have the largest
amount away from one.
Students who do not have experiences with concrete models
like fraction circles or students
who may not have sufficient experiences with models to develop needed mental
representations to judge the relative size of fractions using these informal
strategies make
consistent errors. On the next page we share with you examples of students’
errors based on
written test given to students after their RNP level 1 review lessons. We also
share examples of
correct thinking among this group of sixth graders. In all questions students
were asked to
circle the larger of the two fractions.
Misunderstandings
Students often focus on the denominator only after
internalizing the relationship between the
size of the denominator and the size of the fractional part. To understand what
a fraction
means, students need to coordinate the numerator and denominator - an idea the
following
students did not do.

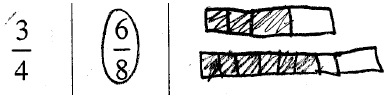
An underlying assumption when ordering fractions is that
the units for both fractions must be
the same. Not realizing the unit needs to be the same is a common error as shown
in this
student’s picture.
Whole number thinking also dominates students thinking
when they first start working with
fractions. This is shown in different ways . Without models students might say
that 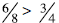
because 6>3 and 8>4. But even after students use concrete models, their whole
number
thinking may still dominate. In the following examples, note that some students
determine the
larger fraction by deciding which fraction had the larger number of pieces. In
other cases,
students look at the difference between numerator and denominator to identify
the larger
fraction. In both instances, students have yet to focus on the relative size the
fractional part
being examined. These students need more time with concrete models to overcome
their whole
number thinking.
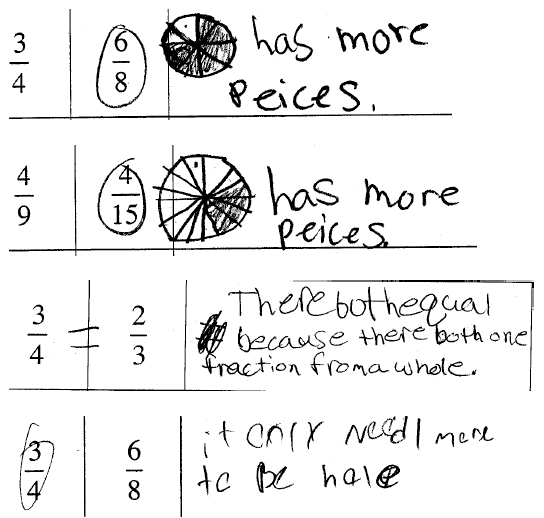
| Prev | Next |
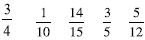
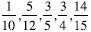
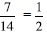 .
.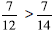 . From this
. From this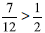 .
. because she knew that
because she knew that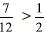 because he doubled the
because he doubled the