Secret of the Universe
Secret of the Universe #1
Hidden within the prime factorization
of any whole number is
its complete set of factors.
Hint: Look for them in pairs.
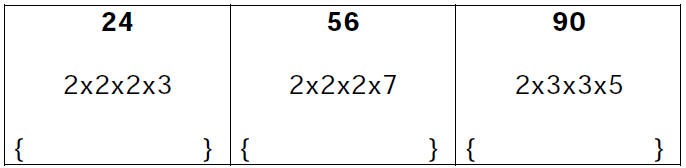
Secret of the Universe #2
The number of factors
in the complete set can be found by:
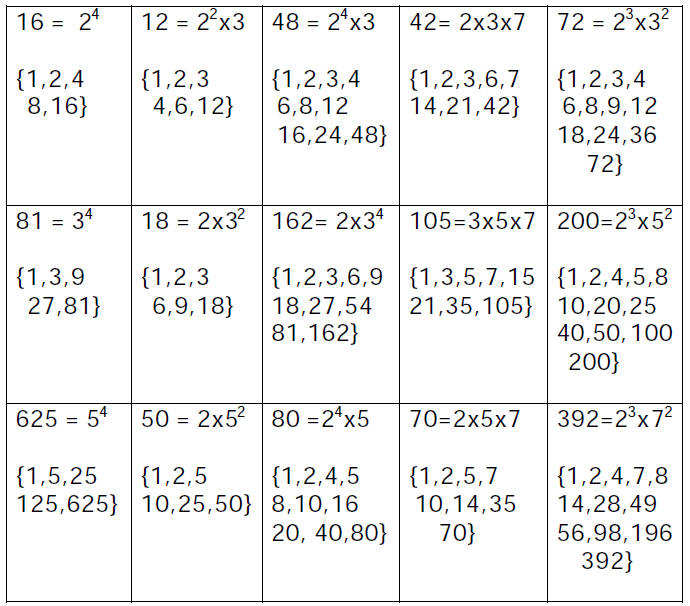
Secret of the Universe #3
The LCM and GCF of two numbers
x and y
are related by the equation :
Secret of the Universe #4
Patterns in Factorizations
The prime factors of perfect squares
Will always have:

Similarly, The prime factors of
perfect cubes Will always

The prime factors of powers of ten
Will always be
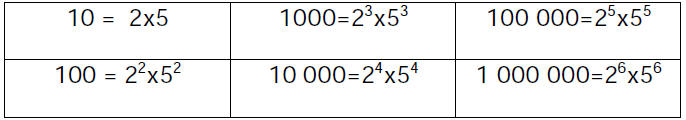
Remember that a factorial has been defined
as follows:
6! = 6x5x4x3x2x1
10! = 10x9x8x7x6x5x4x3x2x1
30! = 30x29x28x27x…x3x2x1
60! = 60x59x58x57x…x3x2x1
If each of the above factorials was written out as
a standard numeral, how many of the last place
values would be occupied by consecutive
zeroes?
Mrs. DeYoung has chartered a chapter of BUNGEE
(Big Unwieldy Number Groups with Excessive Exponents).
The membership requirements for any number have been
established as follows:
1. Only even numbers may be admitted to membership.
2. Each member must be a multiple of 12.
3. Each member must be a perfect square .
4. Each member must possess least 1000 factors .
5. If a member chooses to appear as a standard numeral, the
member is responsible for enforcing the proper “dress
uniform.” (“Dress uniform” is decided by the number of zeroes
at the end of the line . Exactly four terminal zeroes must be
showing at all times to be proper .)
Your task, as representatives of the membership committee,
is
to determine whether the following number groups satisfy the
BUNGEE membership requirements. For applicants that fail to
meet the requirements on the first try, please give them
appropriate constructive criticism. Explain to them exactly
which primes they should “recruit” prior to their reapplication.
Please note that Hope College is committed to nondiscrimination
in applying membership status to any number
groups, so your constructive criticism should never suggest
that any prime factors already present be eliminated .
Applicant A: 28x34x54x174
Applicant B: 22x78x114x176x235
Applicant C: 24x78x134x192
Applicant D: 24x38x54x132x97
Applicant E: 35x57x114x132x23
Applicant F: 26x32x54x74x236
Prime Factor Bingo
| A smaller number |
A number with different parity (odd/even) |
A number with exactly 3 matching prime factors |
| A number with exactly 1 matching prime factor |
FREE | A larger number |
| A number with NO matching prime factors |
The same number |
A number with exactly 2 matching prime factors |
Materials needed: Students each receive the same set of
cubes from which to
select exactly five to make a “special number.” These five are then stacked
(multiplied) to make the individual student’s numbers. I usually give each
student
a stack of 5 red, 5 blue, 2 green and 2 yellow cubes (or 25x35x52x72)
Some possible choices:
2x2x2x2x5 = 80
2x3x3x5x7 = 630
2x3x5x7x7 = 1470
The play: Students circulate to compare numbers and
initial each other’s papers
in the appropriate spaces. Each space must contain a different signature . The
word “matching” means a one-to-one match of cubes (or primes).
Some discussion questions:
What is the largest possible “5-cube number”?
What is the smallest possible “5-cube number”?
How are the primes related to what makes individual numbers larger or smaller?
Do more people have odd numbers or even numbers? Why?
Could any of our numbers be perfect squares ?
Could any of our numbers be powers of ten?
| Prev | Next |