Solutions to Math Homework 1
1 Problem 1
The algorithm will print GCD and LCM of X and Y .
To prove: GCD(X,Y) is given by
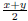while LCM(X,Y) is given by
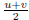
Proof: Invariant for GCD computation are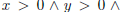 
GCD(X, Y ) =
GCD(x, y). Verify both steps maintain this invariant using the number theory
result that GCD(x,y) = GCD(x-y,y) = GCD(x,y-x). At termination we have
x = y and therefore GCD(x, y) = GCD(x, x) =
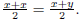
Invariant for LCM computation is uy +vx. Verify that both
steps of algorithm
maintain uy+vx as invariant. Therefore from the initialization conditions when
algorithm terminates uy+vx = XY +XY . Now since x = y = GCD(X, Y ) we
get
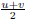× GCD(X, Y ) = XY . Using the number theory result we know that
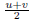is the LCM.
2 Problem 2(0.1)
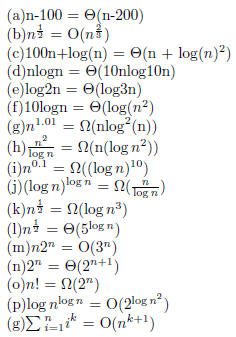
3 Problem 3(0.2)
The given function g(n) turns out to be a geometic series
and it evaluates to
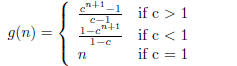(1)
(a) When c < 1, lower bound on Equation 1 can be obtained
by analyzing the
case when n = 0 which is 1. Similarly upper bound is obtained by analyzing
the case when n → ∞ which comes out to be
.
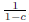Since we got two constants
bounding Equation 1 g (n) is Ө(1)
(b) When c > 1 similar analysis will produce upper and
lower bounds as cn
which makes g(n) as Ө(cn)
(c) When c = 1, the bound of Ө(n) is straight forward as
each term of g(n)
evaluates to 1 and there are n terms.
4 Problem 4(0.3)
(a) Base case :
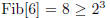
Hypothesis :
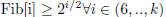
Induction :
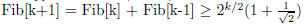
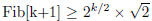
Therefore
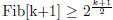
(b) Using the generating function derivation shown in class Fibonacci numbers
can be represented as
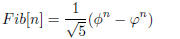(2)
where
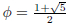and
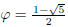Now choosing c as log
ø we need to prove that
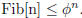We use induction to prove that.
Base case :
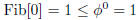
Hypothesis :
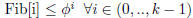
Induction :
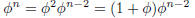
Using induction hypothesis
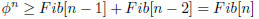
Therefore c is given as log ø
(c)Any number in between 0.5 and logø will suffice. Largest is logø .
5 Problem 5(1.31)
(a) N is an n-bit number. N! is given by 1.2.3...N.
Upper Bound : Assuming each number 1,2,3,...,N is represented by n bits, the
result of multiplying N n -bit number will give a number of N n bits where
N = 2n. Hence it is O(N*n)
Lower Bound : Since each number i
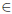(1, 2, ...,N) can be optimally represented
by log i bits , total number of bits in N! is given by
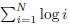which is log N !.
Using Sterling’s approximation or using a factor argument we know
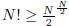
which implies that total number of bits in N! is lower bounded by N log N. It
turns out to be
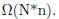Combining both we get ө(N*n)
(b) A simple iterative algorithm to solve the problem is given by:
Input : N
Output : N!
prod = 1
for i = 1 to N
prod = prod * i
return prod
Complexity analysis :We present a worst case bound. Assuming each of the
number 1,2,3,...,N are n-bit long each multiplication computes product of a
i ×n bit number with n bit number. Therefore total time taken by the for-loop
is given by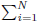
(n × in) which turns out to be O(N2 × n2)
6 Problem 6(1.32)
Given numbers X and Y, apply Euclid algorithm (page 20) to compute GCD(X,Y).
Followed by that get LCM(X,Y) by
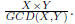GCD computation takes O(n3)
where n are the number of bits in X, Y. Final LCM computation takes O(n2).
Therefore the algorithm is bounded by O(n3).
| Prev | Next |