THE QUADRATIC
§1. Exercises on Basic Properties
1.1. Let f(x) be a quadratic polynomial and suppose that
we divide it by x − u and obtain a remainder r,
where u and r are constants: f(x) = (x − u)g(x) + r.
(a) Explain why the degree of g(x) is 1.
(b) Prove that r = f(u).
(c) Prove that u is a root of the equation f(x) = 0 if and only if there is a
linear polynomial g(x) for
which f(x) = (x − u)g(x).
1.2. (a) How many different quadratic polynomials f(x) can you find for which
f(0) = 5, f(1) = 3 and
f(2) = −7? Determine all of them.
(b) Determine all of the polynomials g(x) of degree not exceeding 2 for which
g(−3) = 2, g(−1) = −1
and g(4) = 0.
1.3. (a) Suppose that f(x) and g(x) are two polynomials of degree not exceeding
2 for which f(u) = g(u),
f(v) = g(v) and f(w) = g(w) for three distinct numbers u , v and w. Prove that
f(x) and g(x) must be
the same polynomial.
(b) Suppose that h(x) is a quadratic polynomial that vanishes at the two
distinct numbers u and v, i.e.,
h(u) = h(v) = 0. Prove that h(x) must be a constant multiple of (x − u)(x − v).
(c) Let a, b, c be three distinct numbers. Determine a quadratic polynomial h(x)
for which h(a) =
h(b) = 0 and h(c) = 1.
1.4. (a) Suppose that a, b and c are three distinct numbers and that f(x), g(x)
and h(x) are quadratic
polynomials for which
h(a) = h(b) = g(a) = g(c) = f(b) = f(c) = 0
and
f(a) = g(b) = h(c) = 1 .
Let p(x) = uf(x) + vg(x) + wh(x) for some constants u, v
and w. Determine the values of p (a), p(b)
and p(c).
(b) Suppose that p(x) is a polynomial of degree less than three for which p(a),
p(b) and p(c) are specified.
Prove that, for every x,
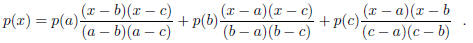
(c) Use the format of (b) to determine the polynomials f(x)
and g(x) asked for in Exercise 1.2. Check
that you get the same answer as you did before.
(d) Use (b) to give a necessary and sufficient condition involving an arbitrary
set {a, b, c} of numbers
that a polynomial p has degree strictly less than 2. [Hint: Look at the
coefficient of x 2 in (b).]
1.5. (a) For each of the quadratic polynomials
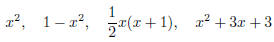
construct a table listing in order nonnegative integral
values of x, the corresponding values of the
polynomial and the difference between the values of the polynomials at
consecutive integers. What do
you notice about the sequence of differences? If you take differences of
consecutive differences, what
happens?
(b) Let p(x) = ax2 + bx + c be a general quadratic polynomial. Verify that, if
q(x) = p(x + 1) − p(x)
and r(x) = q(x + 1) − q(x), then q(x) is a linear polynomial and r(x) is a
constant polynomial.
(c) It is given that f(x) is a quadratic polynomial. Fill in the missing entries
in the following table:
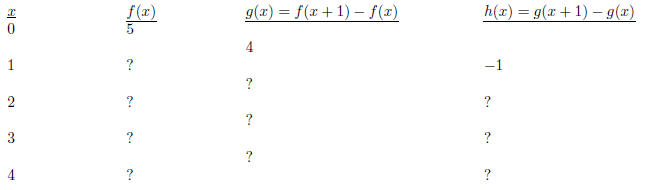
What do you think f(x) is?
1.6. Let p(x), q(x), r(x) be as given in Exercise 1.5.(b). Suppose that p(0),
q(0) and r(0) are given.
(a) Prove that, for each positive integer n,
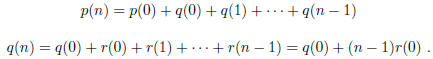
(b) Determine a formula for p(n) in terms of p(0).
1.7. (a) Show that for every quadratic equation (x − p)(x − q) = 0, there exist
constants a, b, c with c ≠ 0
such that (x − a)(b − x) = c is equivalent to given equation and the faulty
reasoning “either x − a or
b − x must equal c” yields the correct answer “x = p or x = q”.
(b) Determine constants a, b, c with c ≠ 0 so that the equation (x−19)(x−97) =
0 can be “solved” in
such a manner.
(International Mathematical Talent Search, Round 25.)
1.8. (a) Write down some values of the polynomial x2 +x+1 for x = 0, 1, 2, 3, ·
· ·. Observe that the product
of two consecutive values in the list occur elsewhere in the list. Formulate and
prove a general result.
(b) Answer (a) for the polynomial x2 + x = x(x + 1).
(c) Any integer that is the product of two consecutive integers is called
oblong. Part (b) can be used to
show that there are infinitely many triples (a, b, c) of oblong numbers for
which c = ab. Investigate the
existence of triples of oblong numbers no two of which are consecutive but for
which the product of two
of them is equal to the third.
1.9. Let p(x) be a monic quadratic polynomial. (This means that the leading
coefficient is 1, so that it has
the form p(x) = x2 + bx + c.) Suppose also that its coefficients are integers.
(a) Prove that there exists an integer k such that
p(0)p(1) = p(k). How many possible such values of k
are there?
(b) More generally, prove that for each integer n, there is at least one integer
m for which p(n)p(n+1) =
p(m).
(c) Are there any values of n for which the value of m determined in (b) is
unique?
1.10. Does there exist a quadratic polynomial f(x) with integer coefficients and
the unusual property that,
whenever x is a positive integer which consists only of 1’s, then f(x) is also a
positive integer consisting
only of 1’s (where the representation is to base 10)?
§2. Exercises on Completing the Square and Transformations
2.1. Let f(x) be a real-valued function.
(a) Compare the graphs of the equations y = f(x) and y = f(2x).
(b) Compare the graphs of the equation y = f(x) and y = 4f(x).
(c) Corroborate your answers to parts (a) and (b) with the example f(x) = x2.
2.2. Let ax2 + bx + c be a quadratic polynomial with real coefficients.
(a) Verify that it equals
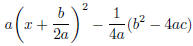
(b) From (a), argue that, when a > 0, the quadratic
assumes its minimum value when x = −b/2a, while
if a < 0, it assumes its maximum value when x = −b/2a.
(c) Use this to describe a transformation in the plane that takes the graph of
the equation
y = ax2 + bx + c
to the graph of the equation y = x2.
2.3. Is it true that all parabolas are the same shape? Explain.
2.4. One geometric definition of a parabola is that it is the locus of points
whose distance from a fixed point
(the focus) is equal to its distance from a fixed line (the directrix). It is
asserted that the graph of the
equation y = ax2 + bx + c is a parabola. Is this consistent with the geometric
definition? If so, what is
the focus? What is the directrix? Look first at some special cases, such as y =
x2, y = x2 + c, y = ax2,
y = x2 − 3x + 2.
§3. Exercises on Solutions of Quadratics
3.1. Let m and n be the solutions of the quadratic equation x2 + bx + c = 0.
Show that b and c are the
solutions of the quadratic equation x2 + (m + n − mn)x − mn(m + n) = 0.
3.2. Suppose that a ≠ c and that x = (b − d)/(a − c) satisfies one of the
equations x2 − ax + b = 0 and
x2 − cx + d = 0. Prove that this value of x satisfies the other.
3.3. Let p(x) and q(x) be two quadratic polynomials with integer coeffients.
Suppose that there is an
irrational number c for which p(c) = q(c) = 0. Prove that one of the polynomials
p(x) and q(x) is a
constant multiple of the other.
3.4. Let p(x) = x2 + bx + c. Suppose that p(0) and p(1)
are solutions of the quadratic equation p(x) = 0.
What are the possible values of the pair (b, c)?
3.5. (a) Show that, for every quadratic equation (x − p)(x − q) = 0, there exist
constants a, b, c with c ≠ 0
such that (x − b)(b − x) = c is equivalent to the original equation and the
following reasoning “either
x − a or b − x must equal to c” yields the correct answers “x = p or x = q”.
(b) Determine constants a, b, c with c ≠ 0 so that the equation (x−19)(97−x) =
0 can be “solved” in
this manner.
[Round 25 of the International Mathematical Talent Search.]
3.6. Suppose x and y are integers. Solve the equation
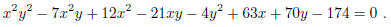
[Problem 2332 from Crux Mathematicorum.]
3.7. Two nested concentric rectangles, are given, with corresponding sides
parallel and each side of the inner
rectangle the same distance from the corresponding side of the outer.
(a) Prove that, if the area of the inner rectangle is exactly half that of the
outer rectangle, then the
perimeter of the inner rectangle is equal to the sum of the lengths of the
diagonals of the outer rectangle.
(b) Verify the result in (a) when the outer rectangle has dimensions 3 × 4, 8 ×
15 and more generally
(m2 − n2) × 2mn where m and n are positive integers.
§4. Exercises on Inequalities
4.1. Let a and b be positive real numbers. Using the fact that the quadratic
equation 0 = (x − a)(x − b) =
x2−(a+b)x+ab has real roots and the discriminant condition, verify the
Arithmetic-Geometric Means
Inequality
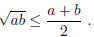
When does equality occur?
4.2. (a) Suppose that a, b, c, u, v ,w are real numbers. Using the fact that the
quadratic polynomial
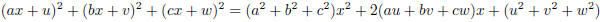
is always nonnegative, argue that it has either coincident
real roots or nonreal roots. Use the discriminant
condition for this to obtain the Cauchy-Schwarz Inequality
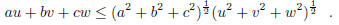
When does equality hold?
(b) Generalize (a) to obtain an inequality for
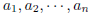 and
and 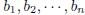
§5. Exercises on Sum and Product of Roots
5.1. The roots of the quadratic equation x2 + bx + c = 0 are m and n. Verify
that b and c satisfy the
quadratic equation x2 + (m + n − mn)x − mn(m + n) = 0.
5.2. (a) Determine any solution in positive integers to the diophantine equation
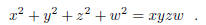
(b) It is possible to show that the diophantine equation
in (a) has infinitely many solutions in positive
integers by the following argument. Suppose that we have found a solution (x, y,
z, w) = (a, b, c, d).
Consider the quadratic equation
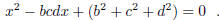
One root of this equation is the integer a. Argue that
there is a second root a' which is also an integer.
Show that (x, y, z, w) = (a', b, c, d) is another solution of the equation in
(a). Use this strategy, starting
with the solution you found in (a), to obtain a sequence of different solutions
to the equation.
| Prev | Next |