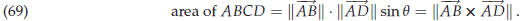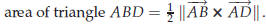Vectors
![]() 44.3 Example.
Let
44.3 Example.
Let 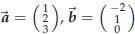 and compute the cross product of
these vectors.
and compute the cross product of
these vectors.
Solution :

![]()
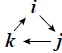 |
In terms of the standard basis vectors you can check the multiplication
table. An easy way to remember the multiplication table is to put the vectors 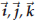 clockwise in a circle . Given two of
the three clockwise in a circle . Given two of
the threevectors their product is either plus or minus the remaining vector. To determine the sign you step from the first vector to the second, to the third: if this makes you go clockwise you have a plus sign, if you have to go counterclockwise, you get a minus. |
The products of 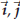 and
and
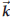 are all you need to know to compute the
cross product. Given two vectors
are all you need to know to compute the
cross product. Given two vectors
![]() and
and![]() write them as
write them as 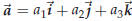 and
and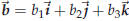 ,
and multiply as follows
,
and multiply as follows
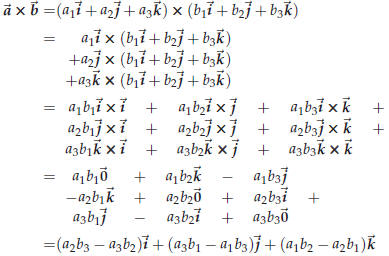
This is a useful way of remembering how to compute the
cross product, particularly when many of the
components 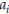 and
and
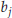 are zero.
are zero.
![]() 44.4 Example.
Compute
44.4 Example.
Compute 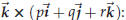
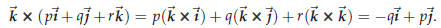
![]()
There is another way of remembering how to find ![]() ×
×![]() . It involves the
“triple product” and
. It involves the
“triple product” and
determinants. See § 44.3.
44.2. Algebraic properties of the cross product
Unlike the dot product, the cross product of two vectors behaves much less like
ordinary multiplication.
To begin with, the product is not commutative – instead one has
 for all vectors
for all vectors ![]() and
and![]() .
.
This property is sometimes called “anti-commutative.”
|
Since the crossproduct of two vectors is again a vector you can compute
the cross product of three vectors  You now have a choice: do
you first multiply You now have a choice: do
you first multiply  , or , or 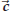 ? With ? Withnumbers it makes no difference (e.g. 2× (3 × 5) = 2 ×15 = 30 and (2 × 3) ×5 = 6 ×5 = also 30) but with the cross product of vectors it does matter: the cross product is not associative, i.e.
|
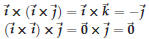 so"×” is not associative |
The distributive law does hold, i.e.
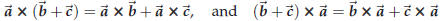
is true for all vectors 
Also, an associative law, where one of the factors is a number and the other two
are vectors, does
hold. I.e
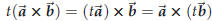
holds for all vectors![]() ,
,![]() and any number t. We were already using these properties when we multiplied
and any number t. We were already using these properties when we multiplied
 in the previous section.
in the previous section.
Finally, the cross product is only defined for space vectors, not for plane
vectors.
44.3. The triple product and determinants
Definition 44.5. The triple product of three given vectors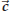 is defined to be is defined to be
|
In terms of the components of ![]() ,
,![]() ,
and
,
and
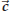 one has
one has
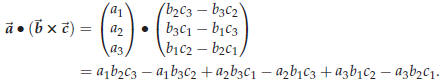
This quantity is called a determinant, and is written as follows
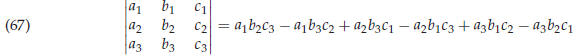
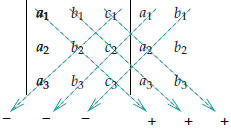 |
There’s a useful shortcut for computing such a determinant: after writing the determinant, append a fourth and a fifth column which are just copies of the first two columns of the determinant. The determinant then is the sum of six products, one for each dotted line in the drawing . Each term has a sign: if the factors are read from top-left to bottom-right, the term is positive, if they are read from top-right to bottom left the term is negative . |
This shortcut is also very useful for computing the cross
product. To compute the cross product of two
given vectors ![]() and
and![]() you arrange their components in the following determinant
you arrange their components in the following determinant
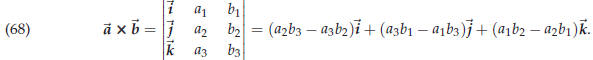
This is not a normal determinant since some of its entries
are vectors, but if you ignore that odd circumstance
and simply compute the determinant according to the definition (67), you
get (68).
An important property of the triple product is that it is much more symmetric in
the factors ![]() ,
,![]() ,
,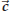
than the notation 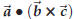 suggests.
suggests.
Theorem 44.6. For any triple of vectors
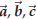 one has
one has
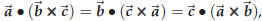
and
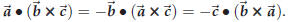
In other words, if you exchange two factors in the product
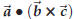 it changes its sign. If you
it changes its sign. If you
“rotate the factors,” i.e. if you replace ![]() by
by![]() ,
,![]() by
by
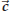 and
and 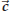 by
by ![]() ,
the product doesn’t change at all.
,
the product doesn’t change at all.
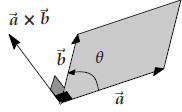
44.4. Geometric description of the cross product
 |
Theorem 44.7.
Proof. We use the triple product:
since |
Theorem 44.8.
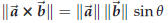
Proof. Bruce just slipped us a piece of paper with the following formula on it:
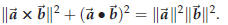
After setting
![]() and
and![]() and
diligently computing both sides we find that this formula
and
diligently computing both sides we find that this formula
actually holds for any pair of vectors ![]() ,
,![]() !
The (long) computation which implies this identity will be
!
The (long) computation which implies this identity will be
presented in class (maybe).
If we assume that Bruce’s identity holds then we get
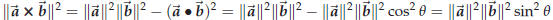
since 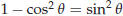 . The theorem is
proved.
. The theorem is
proved.
These two theorems almost allow you to construct the cross product of two
vectors geometrically. If
![]() and
and![]() are two vectors, then their cross product satisfies the following description:
are two vectors, then their cross product satisfies the following description:
(1) If ![]() and
and![]() are parallel, then the angle θ between them vanishes, and so their cross
product is
are parallel, then the angle θ between them vanishes, and so their cross
product is
the zero vector . Assume from here on that![]() and
and![]() are not parallel.
are not parallel.
(2) ![]() ×
×![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() . In other words,
since
. In other words,
since ![]() and
and ![]() are not parallel, they
are not parallel, they
determine a plane, and their cross product is a vector perpendicular to this
plane.
(3) the length of the cross product![]() ×
×![]() is
is 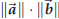 sin θ.
sin θ.
|
There are only two vectors that satisfy conditions 2 and 3: to determine
which one of these is the cross product you must apply the Right Hand Rule (screwdriver rule, corkscrew rule, etc.) for screw moves in the direction of
|
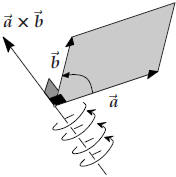 |
45. A few applications of the cross product
45.1. Area of a parallelogram
|
Let ABCD be a parallelogram. Its area is given by
“height times base ,” a formula which should be familiar from high school geometry. If the angle between the sides AB and AD is θ, then the height of the parallelogram is 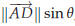 , ,so that the area of ABCD is
The area of the triangle ABD is of course half as much,
|
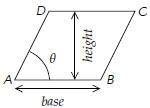 |
These formulae are valid even when the points A, B, C, and D are points in
space. Of course they
must lie in one plane for otherwise ABCD couldn’t be a parallelogram.
| Prev | Next |
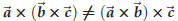 for most vectors
for most vectors 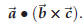
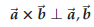
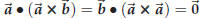
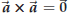 for any
vector
for any
vector