VERIFYING TRIGONOMETRIC IDENTITIES
Fundamental Trigonometric Identities
The Reciprocal and Quotient Identities have been introduced earlier. They will
be presented one
more time because we will have to use them again in our next work. Relearn them
!!!
Reciprocal Identities
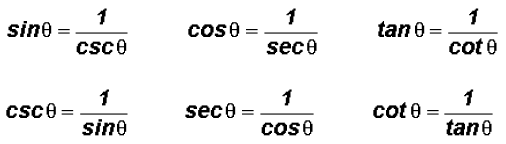
Quotient Identities


Pythagorean Identities
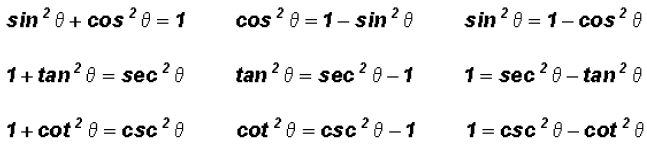
Manipulating Trigonometric Expressions
Please note the following:
1. Adding or subtracting trigonometric expressions:
the common denominator is sin x cos x
to add the two fractions the number 1 has to be multiplied
by cos x and the
expression tan x by sin x, and finally we get
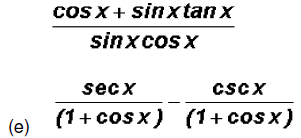
both fractions already have the same denominator, therefore
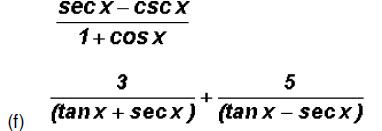
the common denominator is
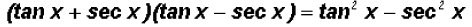
to add the two fractions, the number 3 has to be
multiplied by (tan x - sec x)
and the number 5 by (tan x + sec x)
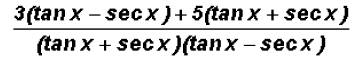
and multiplying out the numerator and combining like terms, we finally get
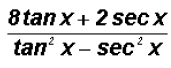
2. Multiplying trigonometric expressions:
(a) Use FOIL to expand the following expression
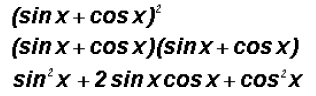
(b) 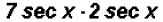 which is equal to
which is equal to
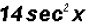
(c) 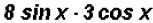 which is equal to
which is equal to
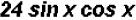
3. Factoring trigonometric expressions:
(a) Factor out the common factor:
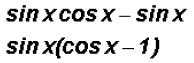
(b) Use the Difference of Squares formula:
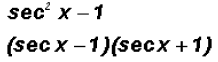
(c) Factor the following expression just like the trinomial 4a2 + a - 3
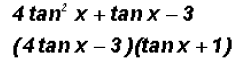
4. Separating rational trigonometric expressions:
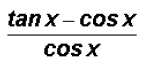
Note: You cannot cancel out cos x in the fraction above.
Only factors can be canceled
in rational expressions.
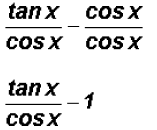
5. Using fundamental identities to rewrite an expression:
(a) rewrite 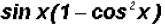
Given the fundamental identity
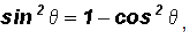
we can rewrite the expression as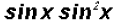 which is
equal to
which is
equal to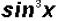
(b) rewrite 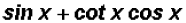
Given the fundamental identity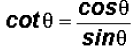
we can rewrite the expression as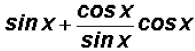
which is equal to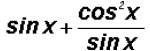
Here we can even do more! How about we find the common
denominator and
then write the expression as a single fraction?
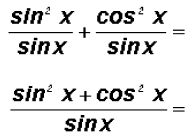
and using the Pythagorean Identity, we get
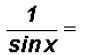
which equals
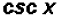
(c) rewrite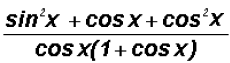
Given the fundamental identity
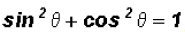 , we can change the
, we can change the
numerator to
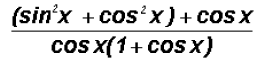
which is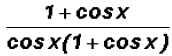
Then we can cancel out the expression
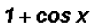 since it occurs both in the
since it occurs both in the
numerator and in the denominator to find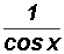 which
equals
which
equals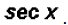
Now that we have learned how to manipulate trigonometric
expressions, we will use these concepts
to verify trigonometric identities that are NOT considered to be "fundamental."
Unfortunately, there are no well-defined rules to follow in verifying
trigonometric identities, and the
process is best learned by practice. There is no right way or wrong way as long
as you follow
established algebra rules.
Besides algebraic rules, there is one rule that you must also follow, and that
is that you must either
change the right side to look like the left side or vice versa. DO NOT WORK ON
BOTH SIDES OF THE
IDENTITY AT THE SAME TIME!
Guidelines for Verifying Trigonometric Identities
• Try to change the side that appears to be the "more complicated" one first.
Note, that "more
complicated" is in the eye of the beholder.
• Use the five (5) manipulations discussed above separately or in combination
with each other .
•
Let the appearance of the "other side" guide you in your decision-making
process!
Example 1:
Verify the identity 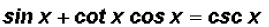
Let's assume that the left side of the identity is the "more complicated" one.
Therefore, we will try to
change it to look like the right side.
What could we do to the left side?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
Let's change cot x to sines and cosines as follows:
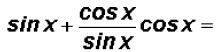
and then we multiply
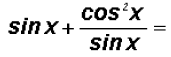
Now what could we do?
1. Add or subtract trigonometric expressions? YES
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
Let's use the common denominator sin x
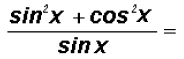
What now?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
Given the Pythagorean Identity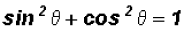 , we can write
, we can write
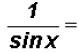
and given the Reciprocal Identity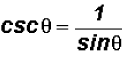 ,
we can show that the left side equals
,
we can show that the left side equals
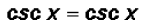
Example 2:
Verify the identity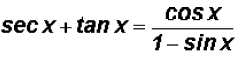
Let's assume that the left side of the identity is the
"more complicated" one. Therefore, we will try to
change it to look like the right side.
What could we do to the left side?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
Let's change the left side to sines and cosines as follows
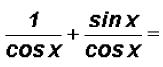
Now what could we do?
1. Add or subtract trigonometric expressions? YES
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
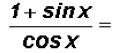
Now, it seems that we are pretty much stuck. There does
not seem to be anything else to do to the
left side. OR?
Actually, there is! Here is a neat little trick for you to add to your bags of
mathematical tricks . That is,
let's change the appearance of the left side by multiplying it by
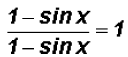
Why would we want to do that? Because we want to think
ahead! The better you get at thinking
ahead, the easier it will be for you to verify identities. Of course, memorizing
the Fundamental
Identities helps tremendously. Let' see what happens:
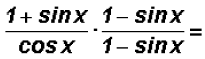
then
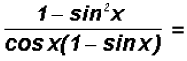
So, what manipulation could we use now to help us along?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
Since we know that 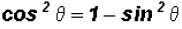 , we can write
, we can write
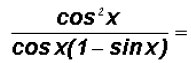
So, what now?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? YES
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
That is, we will factor cos x out of the numerator and the denominator, and we
find that
the left side equals the right side because
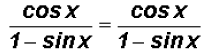
Example 3:
Verify the identity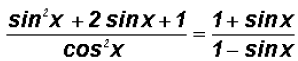
Let's assume that the left side of the identity is the
"more complicated" one. Therefore, we will try to
change it to look like the right side.
Please note that it just so happened that in all three examples the "more
complicated"
side is on the left. This was unintentional and happened purely by chance.
Certainly
identities can be found whose "more complicated" side is on the right side of
the equal
sign . For that matter, all we have to do is switch the sides of the examples
above!
What could we do to the left side?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? YES
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
We will factor the numerator as follows:
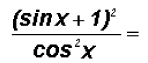
Now what?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We will use the Pythagorean Identity 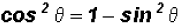 to
rewrite the denominator
to
rewrite the denominator
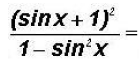
What's next?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? YES
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
Noticing that the denominator is the difference of squares and keeping in mind
of what
the right side looks like, we will factor the denominator:
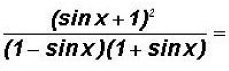
All that's left to do now is to reduce to show that the left side looks like the right side
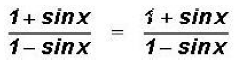
Example 4:
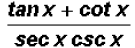 can be reduced to a
single number. Find this number.
can be reduced to a
single number. Find this number.
What could we do?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We can use Reciprocal Identities to rewrite tangent, cotangent, secant, and
cosecant as
follows:
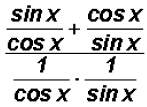
NOTE: While this is certainly a good start, it does not
guarantee success. We
might have to give up and think of something else to do! If you are wondering
if you are ever going to have to use this, wait until you get to calculus. It is
often much easier to reduce a "complicated" trigonometric expression to a
single trigonometric ratio when working with calculus concepts.
Since we learned in algebra to always simplify complex fractions, we will
multiply both the
numerator and the denominator by the LCD sin x cos x just like we used to do in
algebra.
But before we do this, let's combine the fractions in the numerator of the
complex fraction
as follows:
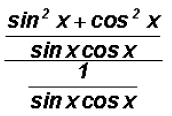
now
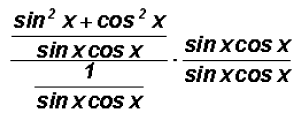
Next, we will distribute and at the same time reduce just like we learned in algebra to get
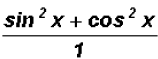
Now what?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We know that 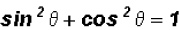 (Pythagorean Identity),
therefore,
(Pythagorean Identity),
therefore,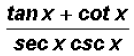
can be reduced to the number 1.
Example 5:
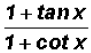 can be reduced to a
single trigonometric ratio, such as cos(x), sin(x), tan(x), sec(x), csc(x),or
cot(x). Find this ratio.
can be reduced to a
single trigonometric ratio, such as cos(x), sin(x), tan(x), sec(x), csc(x),or
cot(x). Find this ratio.
What could we do?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We can use Reciprocal Identities to rewrite tangent and cotangent as follows:
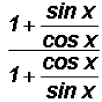
Since we learned in algebra to always simplify complex
fractions, we will multiply both the
numerator and the denominator by the LCD sin x cos x just like we used to do in
algebra
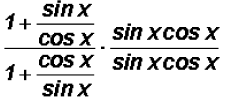
Next, we will distribute and at the same time reduce just like we learned in algebra to get
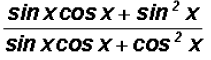
Now what?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? YES
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
Let's factor common factors out of the numerator and the denominator for a lack
of
anything better to do.
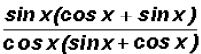
As you can see, the numerator and denominator have a
factor in common and when
reduced we end up with
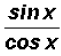 . Finally, we do know that this equals
. Finally, we do know that this equals
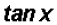 .
.
Therefore, we were able to reduce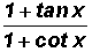 to the single trigonometric ratio
to the single trigonometric ratio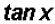
Example 6:
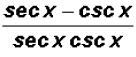 can be reduced to a
difference of two trigonometric ratios. Find this difference.
can be reduced to a
difference of two trigonometric ratios. Find this difference.
What could we do?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We can use Reciprocal Identities to rewrite secant and cosecant as follows:
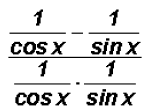
Since we learned in algebra to always simplify complex
fractions, we will multiply both the
numerator and the denominator by the LCD sin x cos x just like we used to do in
algebra.
But before we do this, let's combine the fractions in the numerator of the
complex fraction
as follows:
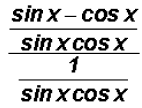
Please note that it is not mandatory to write sin x as the
first factor in the product sin x
cos x. However, it has become "unofficial" standard practice to do so!
Next,
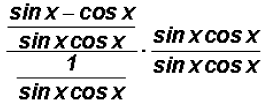
Finally, we will distribute and at the same time reduce
just like we learned in algebra to
get
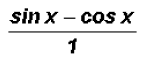
We find that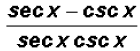 can be
reduced to the difference
can be
reduced to the difference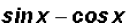 .
.
| Prev | Next |