Continued Fractions and the Euclidean Algorithm
7 Bezout’s Identity and the double recursion
It has already been observed that the process of finding the continued fraction
expansion of a
rational number a/b (b > 0), involves the same series of long divisions that are
used in the
application of the Euclidean algorithm to the pair of integers a and b. Recall
that at each
stage in the Euclidean algorithm the divisor for the current stage is the
remainder from the
previous stage and the dividend for the current stage is the divisor from the
previous stage, or,
equivalently, the dividend for the current stage is the remainder from the
second previous stage.
The Euclidean algorithm may thus be viewed as a double recursion that is used to
construct
the sequence of remainders. One starts the double recursion with
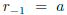and 
.
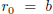At the jth stage one performs long division of
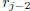by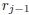 
to obtain the
integer quotient 
and the integer remainder
that satisfies 
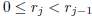. Thus,
The Euclidean algorithm admits an additional stage if
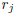> 0. Since
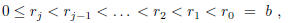
there can be at most b stages.
One may use the sequence of successive quotients
(j ≥ 1) to form
sequences 
and
,
as in the previous section, according to the double recursions:
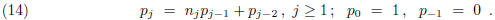
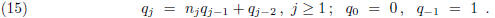
It has already been observed that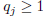 
for j ≥1
and
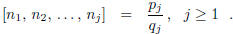
Bezout’s Identity says not only that the greatest common divisor of a and b is
an integer linear
combination of them but that the coefficients in that integer linear combination
may be taken,
up to a sign , as q and p.
Theorem 5. If the application of the Euclidean algorithm to a and b (b >
0) ends with the
mth long division, i.e.,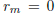 
, then
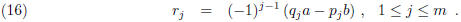
Proof. One uses induction on j. For j = 1 the statement is
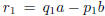. Since by (14,
15) 
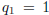and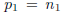 
,
this statement is simply the case j = 1 in (13). Assume j ≥ 2,
and that the formula (16) has been established for indices smaller than j. by
(13) one has
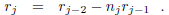
In this equation one may use (16) to expand the terms
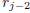and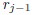 
to
obtain:
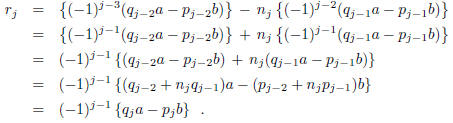
Corollary 3. The greatest common divisor d of a and b is given by the
formula
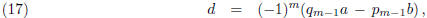
where m is the number of divisions required to obtain zero remainder in the
Euclidean algorithm.
Proof. One knows that d is the last non-zero remainder
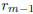in the Euclidean algorithm. This
formula for d is the case j = m − 1 in (16).
Corollary 4.
.
Proof. The last remainder
. The case j = m in (16) shows that
.
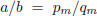Since, by the first proposition of the preceding section,
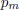and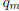 
have no
common factor , this
corollary is evident.
8 The action of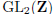 
on the projective
line
If a, b, c, d are real numbers with ad − bc ≠ 0 and
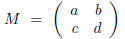
is the matrix with entries a, b, c, and d, then M · z, for z real, will denote
the expression
One calls M · z the action of M on z.
M · z is a perfectly good function of z except for the case z = −d/c where the
denominator
cz + d vanishes. If it were also true that az + b = 0 for the same z, then one
would have
−b/a = −d/c, in contradiction of the assumption ad − bc ≠ 0. Thus, when z =
−d/c, the
value of |M ·w| increases beyond all bounds as w approaches z, and it is
convenient to say that
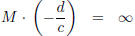
where ∞ is regarded as large and signless. If further it is agreed to define
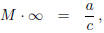
which is the limiting value of M · w as |w| increases without bound, then one
may regard the
expression M · z as being defined always for all real z and for ∞. The set
consisting of all real
numbers and also the object (not a number) ∞ is called the projective line. The
projective line
is therefore the union of the (ordinary) affine line with a single point ∞.
Proposition 4. If 
is any continued fraction, then
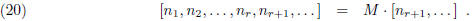
where
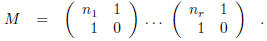
Proof. Let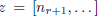 
. Then
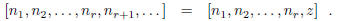
The statement of the proposition now becomes
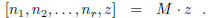
This may be seen to follow by multiplying both sides in formula (9), after
replacing 
with
,
by the column
The matrix M in the preceding proposition is an integer matrix with determinant
±1. The
notation 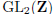denotes the set of all such matrices. (The 2 indicates the size
of the matrices,
and the Z indicates that the entries in such matrices are numbers in the set Z
of integers.) It
is easy to check that the product of two members of 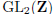is a member of
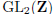and that
the matrix inverse of a member of 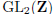is a member of 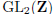. Thus,
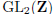forms
what is called a group . The formula (19) defines what is called the action of
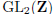on the
projective line.
One says that two points z and w of the projective line are rationally
equivalent if there is a
matrix M in 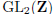for which w = M · z. Since (i)
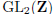is a group, (ii) 
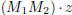, and (iii) w = M · z if and only z = M-1 ·w, it is easy to see that
every point of
the projective line belongs to one and only one rational equivalence class and
that two points
rationally equivalent to a third must be rationally equivalent to each other.
Terminology. The rational equivalence of points on the projective line is said
to be the equivalence
relation on the projective line defined by the action of .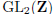
Example 1. The set of real numbers rationally equivalent to the point 1 is
precisely the set
of rational numbers.
Example 2. The proposition above shows that any continued fraction is rationally
equivalent
to each of its tails. It follows that all tails of a continued fraction are
rationally equivalent to
each other.
9 Periodic continued fractions
In one of the first examples of a continued fraction expansion, it was shown
that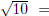 
[3, 6, 6, 6, . . . ]. This is an example of a periodic continued fraction. After
a finite number of
terms the sequence of integers repeats cyclically. If a cyclic pattern is
present from the very first
term, then the continued fraction is called purely periodic. Evidently,
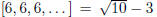
is an example of a purely periodic continued fraction.
Note that a periodic continued fraction cannot represent a rational number since
the continued
fraction expansion of a rational number is finite.
Theorem 6. Every periodic continued fraction is the
continued fraction expansion of a real
quadratic irrational number.
Proof. For clarity: it is being asserted that every periodic continued fraction
represent a number
of the form
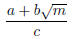
where a, b, c, and m are all integers with m > 0, c ≠ 0, and m not a perfect
square .
Numbers of this form with fixed m but varying integers a, b, and c ≠ 0 may be
added, subtracted,
multiplied, and divided without leaving the class of such numbers. (The
statement
here about division becomes clear if one remembers always to rationalize
denominators.) Consequently,
for M in 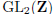the number M · z will be a number of this form or
∞ if and only
if z is in the same class.
Since a periodic continued fraction is rationally equivalent to a purely
periodic continued fraction,
the question of whether any periodic continued fraction is a quadratic
irrationality reduces
to the question of whether a purely periodic continued fraction is such. Let
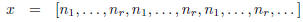
be a purely periodic continued fraction. By the proposition of the preceding
section, x = M· x
where M is notationally identical to the M in (20). Ignoring the computation (9)
of M in
terms of convergents, let
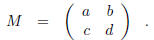
Then
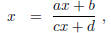
or, otherwise said, x is a solution of the quadratic equation
cx2 − (a − d)x − b = 0 .
Remark 2. It is conversely true that the continued fraction expansion of every
real quadratic
irrationality is periodic.
This converse will not be proved here.
| Prev | Next |