10350 Tutorial Week 10 - Set 01 Solutions
10350 Tutorial Week 10 - Set 01
1a. Find all critical points of
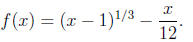
Solution . We have
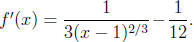 This is undefined for x = 1, and we have
This is undefined for x = 1, and we have
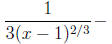
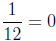 gives (x -1)2/3 = 4, so (x -1)1/3 = ±2, thus x = -7, 9,
thus our critical points are at x = -7, 1, 9.
gives (x -1)2/3 = 4, so (x -1)1/3 = ±2, thus x = -7, 9,
thus our critical points are at x = -7, 1, 9.
1b. Find the absolute maximum and absolute minimum of
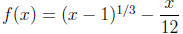 for -7 ≤ x ≤ 28.
for -7 ≤ x ≤ 28.
Solution .
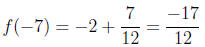
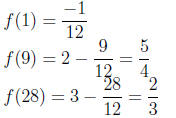
This gives our absolute maximum of 5/4 at x = 9, and the absolute minimum of
-17/12 at x = -7 (note
that all four points to check are in the domain -7 ≤ x ≤ 28).
10350 Tutorial Week 10 - Set 02
1a. Find all critical points of
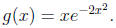
Solution .
 , which is defined for all x.
, which is defined for all x.
Then
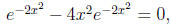 so
so
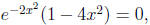 so 1 - 4x2 = 0, so x2 = 1/4, so x = ±1/2 are the
critical
so 1 - 4x2 = 0, so x2 = 1/4, so x = ±1/2 are the
critical
points of g(x).
1b. Find the absolute maximum and absolute minimum of
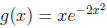 for 0 ≤ x ≤ 1.
for 0 ≤ x ≤ 1.
Solution . f(0) = 0
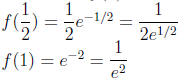
This gives the absolute maximum of
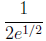 at x = 1/2 and the absolute minimum of 0 at x = 0. Note
at x = 1/2 and the absolute minimum of 0 at x = 0. Note
that we don't consider x = -1/2 since it is not in the given domain of 0 ≤ x ≤
1.
10350 Tutorial Week 10 - Set 03
1. At noon, ship A is 10 km due East of ship B. Ship A is sailing west at 3
km/hr, and ship B is sailing
south at 1 km/hr. At what time will the ships be nearest to each other, what
will this distance be?
Solution . We can assume that ship B is at the
origin at time 0, and ship B is then 10 miles east of
the origin. Note that they start out 10 km from each other (this is the endpoint
for t = 0). We know
that at time t, we have ship B is t units south of the origin and ship A is 10 -
3t units from the origin.
If c is the distance between them, we have (from the Pythagorean Theorem) c2 =
(10 - 3t)2 + t2, or
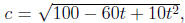 so by the chain rule
so by the chain rule
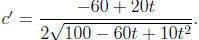 The function is undefined when
The function is undefined when
the denominator is zero , so when 100 - 60t + 10t2 = 10(10 - 6t + t2) = 0, or
10 - 6t + t2 = 0, but the
discriminant (the part under the square root in the quadratic formula, b2-4ac)
is (-6)2-4(1)(10) = -4,
hence the quadratic formula gives imaginary answers for x, so the function is
always defined. Thus, we
only need to set c' = 0, giving that the numerator must be 0, so we get 20t - 60
= 0, or t = 3. Since,
at t = 3 our distance is
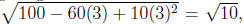 which is less that the distance of 10 at t = 0,
which is less that the distance of 10 at t = 0,
we know our minimum occurs at 3PM with a distance of
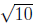 km.
km.
10350 Tutorial Week 10 - Set 04
1. Consider the function f(x) = x ln(x2).
1a. Find the derivative of f(x).
Solution . f'(x) = ln(x2) + 2
1b. Using Q1(a), verify that the function f(x) = x ln(x2)
satisfies the hypotheses of the Mean Value
Theorem on [1, e]. Explain clearly in words.
Solution . Our function f is continuous on [1, e],
and the derivative exists on the interval (1, e).
Thus we can apply the MVT.
1c. Find all numbers c that satisfies the conclusion of the Mean Value Theorem for f(x) = x ln(x2) .
Solution . We need c with
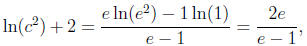 so
so
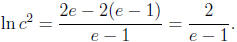
Thus,
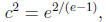 so
so
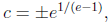 giving the answer (in the domain: [1, e]) of
giving the answer (in the domain: [1, e]) of
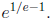
| Prev | Next |