A Construction of the Real Numbers

Distributive law : Let R; S; T be Dedekind positive reals.
Suppose that x ∈ R · (S + T). Then there are u ∈ R and v ∈ S + T
such that u · v = x. Further, there are a ∈ S and b ∈ T such that
a+b = v. So u · (a+ b) = x, so u · a + u · b = x, and, since u · a ∈ R · S
and u · b ∈ R · T, we have x ∈ R · S + R · T.

Now suppose that x ∈ R · S +R · T. It follows that there are u ∈ R · S
and v ∈ R · T such that u + v = x. Further, there is a ∈ R and b ∈ S
such that a · b = u and c ∈ R and d ∈ S such that c · d = v. Here there
is a real obstruction: we would like a to be the same number as c! This
is easily nessed, however. Let e = max(a, c). a · b = e · (b · a · e^-1), and
further e ∈ R and b · a · e^-1 ∈ S (because a · e^-1 ≤ 1 and S is downward
closed). Similarly c d = e (d c e^-1) and d c e^-1 ∈ T. Now we have
x = e · (b · a · e^-1+d · c · e^-1), from which it follows that x ∈ R · (S +T).

This completes the proof of the distributive property.

Identity law : The identity of the Dedekind positive reals is defined as =
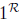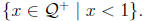Clearly this is a Dedekind real.
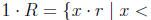
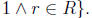Clearly any x · r with x < 1 and r ∈ R itself belongs to R
because R is downward closed and x · r < r. Further, any element r of
R can be written in the form x · r' where x < 1 and r' ∈ r: let r' > r
be any element of R greater than r (R has no largest element) and let

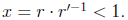
Inverse law: For any Dedekind positive real R, define R^-1 as
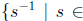
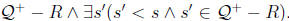Proving that this is a Dedekind
positive real is routine. We outline the proof that 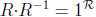, Suppose
that x ∈ R · R^-1. It follows that there are r ∈ R and s 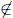R such that
r · s^-1 = x. Since s 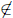R we have s > r so x = r · s^-1 < 1, so x ∈ .
Now suppose that x ∈ , that is, x < 1. We claim that there must be
r ∈ R and s ∈ R^-1 such that r ·s = x, or, equivalently, there must be
r ∈ R such that r ·x^-1 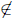R (and further is not the minimal element of
the complement of R, either, but this is easy to arrange by increasing
r slightly). It is sufficient to show that for any fixed x^-1 > 1, any
downward closed set of positive rationals closed under multiplication
by x^-1 is in fact the entire set of positive rationals (the powers of x^-1
are unbounded). This is the reason we stated the Unbounded Powers
property of the positive rationals above, which says exactly this.

Definition of order: We define order on the positive reals exactly as we did
on the positive rationals. R < S is defined as "there exists a positive
real T such that R+T = S". (Here we do not define R ≤ S as R 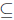S,
though this equivalence is provable as a theorem).

Definition of subtraction : For positive rationals r < s, there is (by deff-
nition of order) t such that r + t = s, and it is fairly easy to show that
this t is unique using our axioms. We define r - s as this t. We want
to extend this definition to positive reals. If R and S are reals (naively
understood) we would like to identify the set of positive reals less than
R - S. A difference of rationals r-s will be less than R - S if r < R
and s > S (not s < S)!

We define R-S as 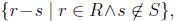for all R and S for which this
set is not empty. Notice that for this set to be nonempty there must
be an element of R which is greater than some non-element of S and
so greater than all elements of S. Further, if there is any element of R
which is not an element of S (and so greater than all elements of S),
it is easy to see that R - S will be nonempty. If this set is nonempty,
it is easy to see that it is a Dedekind positive real. It does not contain
all positive rationals because it is a subset of R. Suppose r ∈ R and
s 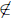S and t < r - s. r - t exists and is greater than s so does not
belong to S: r - (r - t) = t witnesses the fact that t ∈ R - S. r - s
is not the largest element of R - S because we can choose r' > r in R
and r' - s > r - s belongs to R - S.

We claim that (R - S) + S = R if R - S is nonempty. An element of
(R - S) + S is of the form (r - s') + s, where r ∈ R; s' 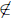  S and s ∈ S.
Since s' > s must be true, we have (r - s') + s < (r - s') + s' = r,
and so (r - s') + s 2 R because R is downward closed. Now let r
be any element of R which is greater than all elements of S: we want
to show r ∈ (R - S) + S (it will follow that all elements of R are in
(R - S) + S). Let r' > r be an element of R. Let s' 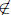s and s ∈S be
such that s' - s ≤ r' - r. It should be clear that s' < r'. [if there were
no such s' and s then the smallest set containing S and closed under
addition of r ' - r would contain only elements of S, contrary to the
Induction Property]. Now we see that (r' - s')+s ≥ r is an element of
(R   S) + S, and so is r.

Trichotomy 1: Let R and S be Dedekind positive reals. Either R = S, in
which case we are done, or either R contains an element not in S or S
contains an element not in R. If R contains an element not in S then
R-S is not empty and S +(R-S) = R, so S < R. If S contains and
element not in R we show R < S in the same way.

Trichotomy 2: Let R and S be Dedekind positive reals. Suppose R < S
and S < R. So we have R + T = S and S + U = R for some T and U,
whence we have R+(T +U) = R. But this means that R is closed as a
set under the addition of elements of T + U, or indeed under addition
of any specific element of T + U, which is impossible by the Induction
Property stated for the positive rationals.

Now we need to show that the positive reals satisfy the Least Upper
Bound Property. For this we need an observation: R < S is true precisely if
S - R is nonempty, which happens precisely if 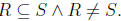So R ≤ S is
precisely equivalent to R 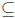S: this is the most convenient way to view it for
proving the L.U.B. property.

Suppose that 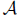is a set of Dedekind positive reals which is nonempty
and bounded above by a Dedekind positive real B. We claim that 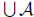is the
least upper bound of .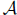

We need to show that 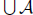is a Dedekind positive real. It is clearly
nonempty, because each element of 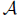is nonempty. It is not the entire set of
positive rationals, because we have A 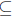B for each A ∈ 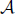, whence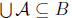
as well, and B is not all of the positive rationals. It is downward closed: if
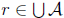and q < r (both positive rationals) then there is 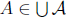such that
r ∈ A, whence q ∈ A, whence q ∈ 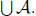. Finally, if r ∈ 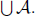, we have r 2 A
for some A ∈ A, whence we have some r' > r with r' ∈ A, whence we have
r' ∈ 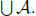as well.

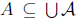is obvious for 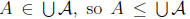for all 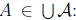the
purported least upper bound is in fact an upper bound. We have already
seen above that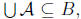where B was an arbitrarily chosen upper bound
of 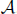, so we have the least upper bound.

What we have constructed so far is just a model of our axioms for the
positive reals. We proceed to complete our task by showing how to get a
model of all the reals, positive and negative .

We only sketch this for now: it looks like the construction of the integers
from the natural numbers on the track the book takes. The general reals
are defined as equivalence classes of ordered pairs of positive reals under the
equivalence relation (m, n) ~ (p, q) defined as m + q = n + p. We need to
verify that this is an equivalence relation.

Then we define [(m, n)]+[(p, q)] = [(m+p, n+q)] and [(m, n)] [(p, q)] =
[(mp + nq, mq + np)]. We define [(m, n)] < [(p, q)] as m + q < n + p. It
is necessary to verify that these definitions do not depend on the choice of
representatives from the equivalence classes.

It is then an exercise in algebra (using additive cancellation to compensate
for the lack of subtraction) to show that this has the properties of a complete
ordered field.