Quadratic Equations

Definitions: Quadratic equation:

(General form)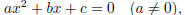

where a, b, c are constants.

Note: If a quadratic equation does not have a general form, we can always rewrite it into a general
form.

E.g.,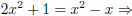

Solving Quadratic Equations

We will only consider real number solutions .

Always modify the equation in general form first. Then use one of two methods :

1. Factoring 2. The quadratic formula

If the given equation is a rational equation , check the values that make the denominator(s) zero so
that you can eliminate them from the solution.

Factoring Method

Zero product property : ab = 0, where a, b are real 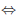a = 0 or b = 0 or both.

Ex.1 (#10) Solve

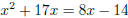
Ex.2 Solve

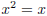
Ex.3 (#16) Solve (x - 3)(1 - x) = 1

Ex.4 (p.142) Solve

The Quadratic Formula

Square root property: The solutions of x² = C is
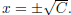
(Or one can think this as factoring

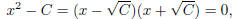
which gives )

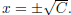Ex.5 (#34) Solve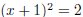

Quadratic Formula : If ax² + bx + c = 0, where a ≠ 0, then

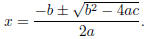
Sign of b 2 - 4ac	Solutions
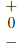	Two distinct real solutions Exactly one real solution No real solutions

Ex.6 (#22) Solve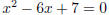

Ex.7 (#24) Solve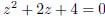

Applications

Note: There may be solutions to a quadratic equation that are not the solutions to a problem.

Ex.8 (#44) If the pro t from the sale of x units of a product is 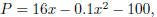what level(s) of
production will yield a pro t of $180?
 

Ex.9 (#48) A tennis ball is thrown into a swimming pool from the top of a tall hotel. The height of the
ball from the pool is modeled by

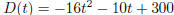feet,

where t is the time, in seconds, after the ball is thrown. How long after the ball is thrown is it 4
feet above the pool?