A Pedagogical Analogy between Forgetful Functors and Certain Polynomials
A Pedagogical Analogy between Forgetful Functors and Certain Polynomials
Introduction
This much, hopefully, is clear enough: Let C and D be
groupoids , and let F be a functor from C to D.
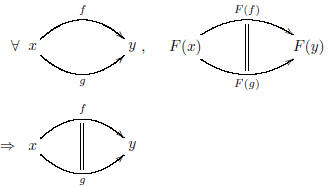
Then F is faithful if, given objects x and y of C and morphisms f and g
from x to y in C, whenever
F(f) and F(g) are equal in D, then f = g back in C.
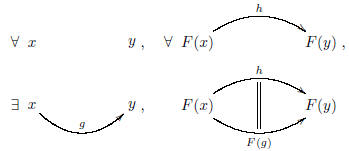
Also, F is full if, given objects x and y of
C, whenever h is a morphism from F(x) to F(y) in D, then
there is a morphism g from x to y back in C such that h = F(g) in D.
Finally, F is essentially surjective if,
whenever z is an object of D, then there is an object y back in C
such that there s a morphism h from z to F(y) in D.
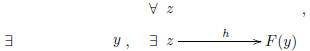
That much, hopefully, is clear enough; and it fits the only obvious pattern.
But now we can define some subsidiary notions: First, F
forgets nothing if it s essentially surjec-
tive, full, and faithful. Next, F forgets only property if it s full and
faithful. Next, F forgets at most
structure if it s faithful. Finally, F forgets at most stuff always.
These form a pattern as well, but it
may not be at all clear why this is a relevant pattern. It also may not be clear
why these are reasonable
names; what do they say about the nature of stuff , structure, and property
themselves?
To answer these questions, I put forward an analogy with certain polynomials.
The analogue
Consider a polynomial P of the form ax2 + bx + c, where
(to be definite) a, b, and c are natural num-
bers. We re all familiar with several useful classes of polynomials: First, P is
zero if a , b, and c are all
zero. Next, P is constant if a and b are both zero. Next, P is linear if a is
zero but b is not. Finally, P
is quadratic if a is not zero .
Actually, the concepts of linear and quadractic
polynomials are somewhat unnatural. They re use-
ful notions in the context of fin ding the roots of polynomials , because we need
something nonzero to di-
vide by. (Think of a's place in the quadratic formula , for example.) But they re
not quite the right sets of
polynomials. (They re not closed under addition, for example.) So to correct
this, let P be at most lin-
ear if a is zero, and let P be at most quadratic always. (Thus the `certain
polynomials' in the title are
in fact the at-most-quadratic polynomials.)
These should still be familiar kinds of polynomials, and
you can see why the definitions should go in
this order, rather than the other order; it s because c really must be the end
of the polynomial, whereas
a (despite getting its name from the beginning of the alphabet by tradition) is
only the beginning of the
polynomial because we restricted attention to at-most-quadratic polynomials.
Clearly, the concept can be
generalised to polynomials of higher degree.
The analogy
Here is the basic idea: In the polynomial ax2 + bx + c,
the coefficient a represents how unfaithful a functor
is, while the coefficient b represents how unfull it is, and the coeffecient c
represents how essentially unsur-
jective it is. Thus the zero polynomial corresponds to an equivalence, a
constant polynomial corresponds
to a full and faithful functor, an at-most-linear polynomial corresponds to a
faithful functor, and an at-
most quadratic polynomial corresponds to an arbitrary functor. But these are
precisely the functors that
we said forgot, respectively, nothing, only property, at most structure, and at
most stuff . So these would
seem to be sensible notions after all.
And what about polynomials of higher degree? They are
generalisations of at-most-quadratic polyno-
mials, and they correspond to generalisations of the notion of functor. Just as
there is no reason to stop
at x2, so there is no reason (in principle) to stop at groupoids. We can go on
to 2-groupoids, 3-groupoids,
and the like; and similarly, we can generalise stuff types to 2-stu types (which
Jim calls `eka-stuff types'),
3-stu types, and the like. So the best thing to learn from the analogy with
polynomials is to realise that
we' ve barely started!
Homogenous polynomials
There is another way to break down the class of
polynomials. This is given by the notion of homogeneous
polynomial, a polynomial each of whose terms has the same degree. Since our
polynomials are in a single
variable , this means that we re basically talking about monomials except that
the zero polynomial is
also included.
The first type of homogeneous polynomial is the constant
polynomial again, one where both a and b
are zero. But the next kind is the homogeneous linear polynomial, where a is
zero (so it is at most
linear) but c is also zero. Finally, we have the homogenous quadratic
polynomial, where b and c are
both zero. Notice that the zero polynomial belongs to each of these groups, but
they are otherwise dis-
joint. And a generic polynomial won t be homogeneous of any degree.
The corresponding types of functors are also interesting.
A functor that is both full and faithful for-
gets only property, as before. But now, a functor that is both essentially
surjective and faithful forgets
purely structure. And a functor that is both essentially surjective and full
forgets purely stuff . An
equivalence is all of these; a generic functor is none of these.
Now, a constant polynomial can be written as c, which is a
single natural number; metaphorically,
we can say that c is the number of properties that the functor forgets.
Similarly, a homogenous linear
polynomial is bx, and we can say (even more metaphorically) that the number b
measures how much pure
structure is forgotten. Finally, a homogenous quadratic polynomial has the form
ax2, and we can say that
a measures how much pure stuff has been forgotten.
There are limits to this analogy. An at-most-quadratic
polynomial may be specified by giving the
numbers a, b, and c independently, but this won t work for a functor. You can' t
simply say , This stuff is
forgotten, also this property; and by the way, we also forget this structure
here. . This is because they are
tied together; you only know what properties are avaiable after the stuff and
structure have been specified.
Conversely, if you forget a structure, then the properites referring to it (if
they can' t be reinterpreted in
terms of surviving structures) become irrelevant. So unlike with polynomials ,
the 3 levels are not indepen-
dent.
Nevertheless, there is a real and important sense in which
an arbitrary functor may be built up in 3 steps ,
just as an arbitrary at-most-quadratic polynomial may be built up in 3 terms.
One just needs to be care-
ful about the order. To deal with this, I must extend the analogy to cover
polynomial addition. Specifical-
ly, the addition of polynomials is analogous to the composition of functors. The
idea to keep in mind here
is that just as the coefficients of P + Q are as big as the coefficients of P and Q
combined , so the functor
F G forgets as much as F and G forget combined.
One relevant property of the natural numbers is that 0 + 0
= 0. Thus a sum of at -most-linear polyno-
mials (meaning that a is zero) is at most linear; similarly, a composition of
forgetting-at-most-structure
functors forgets at most structure (meaning that it s faithful). The same goes
for the full functors, the
forgetting-purely-stuff functors, the forgetting-only-property functors, and so
on. Despite the warning in
the footnote, there is a good reason that I defined my polynomials over the
natural numbers. Recall this
fact about natural numbers: If a + b is zero, then a and b are also both zero. A
consequence for polyno-
mials is that if P + Q is zero, then P and Q are also both zero. This
corresponds to the fact for functors
that if F ◦ G is an equivalence, then F and G are also both equivalences.
Functor factorisation
Now I can tackle the factorisation of functors into
functors that forget purely one level, just as polyno-
mials can be broken down into (homogeneous) monomials . Given groupoids C and D
and a functor F:
C → D, we can break down F as a composition, first of a functor that forgets
purely stuff , then a functor
that forgets purely structure, and finally a functor that forgets only property.
(The order of composition is
important!)
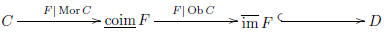
First, let
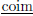 F be the
weak coimage of F, a category
whose objects are the objects of C but whose
F be the
weak coimage of F, a category
whose objects are the objects of C but whose
morphisms come from D; specifically, given objects x and y in C, the morphisms
from x to y in
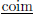 F
F
are those morphisms from F(x) to F(y) in D that lie in the image of F. Then F
induces a functor from C
to
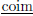 F, which acts like the identity on objects but like F on morphisms. This
functor is essentially sur-
F, which acts like the identity on objects but like F on morphisms. This
functor is essentially sur-
jective and full; it forgets purely stuff . Next, let
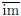 F be the
full image of F
in D; its objects are those
F be the
full image of F
in D; its objects are those
objects of D that lie in the image of F, and its morphisms are all of the
morphisms in D between these
objects. Then F induces a functor from
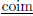 F to
F to
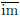 F, which acts like F on
objects but like inclusion
F, which acts like F on
objects but like inclusion
on morphisms. This functor is essentially surjective and faithful; it forgets
purely structure. Finally, the
inclusion of
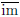 F into D is full and faithful; it forgets only property.
(Incidentally, the image of F never
F into D is full and faithful; it forgets only property.
(Incidentally, the image of F never
shows up itself, since it may not be closed under composition unless F is
injective on objects.)
Summary
The analogy is between at-most-quadratic polynomials over
the natural numbers and functors between
groupoids.
| Polynomials | Functors |
| Zero | Equivalence |
| Constant | Forgets only property |
| At most linear | Forgets at most structure |
| Homogeneous linear | Forgets purely structure |
| Homogeneous quadratic | Forgets purely stu |
| Addition | Composition |
| Sum of homogeneous polynomials: | Composition of purely forgetful functors: |
| P = (ax2) + (bx) + (c) |
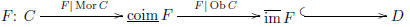 |
| Prev | Next |