Get it on Google Play Get it on Apple Store

Basic Linear Algebra

• A vector b having n components is a linear combination of the k
vectors 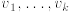, each having n components, if it is possible to find
k real numbers 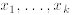satisfying:



To find the numbers 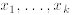, view (1.1) as a system of linear
equations and solve by the Gauss- Jordan method .

• A set of vectors (all having n components) is linearly dependent if
at least one vector is a linear combination of the others. Otherwise
they are linearly independent .

• Given n linearly independent vectors 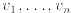, each having n com-
ponents, any desired vector b with n components can be obtained
as a linear combination of them:



The desired weights 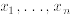are computed by solving (1.2) with
the Gauss-Jordan method: there is a unique solution whenever the
vectors 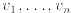are linearly independent.

Exercise 6 A can of Brand A mixed nuts has 1 lb cashews, 1 lb almonds, 2 lb peanuts. Brand B
has 1 lb cashews and 3 lb peanuts. Brand C has 1 lb almonds and 2 lb peanuts. Show how much
of each brand to buy/sell so as to obtain a mixture containing 5 lb of each type of nut.
Exercise 7 Determine whether the vector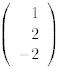is a linear combination of

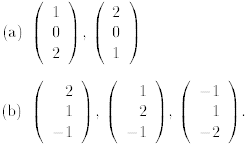
In linear programming, there are typically many more variables than equations. So, this case
warrants looking at another example.

Example 1.3.1 (Basic Solutions.) A craft shop makes deluxe and regular belts. Each deluxe
belt requires a strip of leather and 2 hours of labor. Each regular belt requires a leather strip and
1 hour of labor. 40 leather strips and 60 hours of labor are available. How many belts of either
kind can be made?

This is really a mixing problem. Rather than peanuts and cashews, the mixture will contain
leather and labor. The items to be mixed are four activities: manufacturing a deluxe belt, manu-
facturing a regular belt, leaving a leftover leather strip in inventory, and leaving an hour of labor
idle (or for other work). Just as each Regular can of mixed nuts contributes 1 pound of cashews
and 3 pounds of peanuts to the mixture, each regular belt will consume 1 leather strip and 2 hours
of labor. The aim is to combine the four activities in the right proportion so that 40 strips and 60
hours are accounted for:

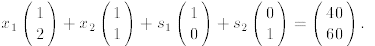
So,

= number of deluxe belts made
= number of regular belts made
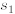= number of leather strips left over
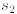= number of labor hours left over

In tableau form, the equations are

Since there are only two equations , you can only solve for two variables. Let's solve for and ,
using Gauss-Jordan elimination. After the first iteration you get,

A second iteration yields the solution,

This tableau represents the equations

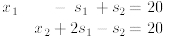
or,

You can't say how many deluxe belts and regular belts the plant will make until you specify
how much leather 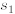and labor 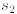will be left over. But (1.6) is a formula for computing how many
belts of either type must be made, for any given 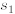and 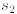. So the equations have many solutions
(infinitely many).

For example, if you want to have nothing left over (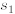 = = 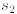0), you will make 20 of each. If
you want to have 5 strips and 5 hours left over, you will make = 20 deluxe and = 15 regular
belts.

The variables , you solved for are called basic variables. The other variables are nonbasic.
You have control of the nonbasic variables. Once you give them values, the values of the basic
variables follow. A solution in which you make all the nonbasic variables zero is called a basic
solution.

Can you have basic variables other than , ? Sure. Any pair of variables can be basic,
provided the corresponding columns in (1.3) are linearly independent (otherwise, you can't solve
for the basic variables).

Equations (1.3), for instance, are already solved in (1.3) for basic variables 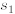, 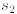. Here the
two basic activities are having leftover leather and having leftover labor. The basic solution is
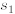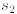(, ) = (40, 60). This means that if you decide to produce no belts ( = = 0), you must have
40 leftover leather strips and 60 leftover labor hours.

The intermediate step (1.4) solves the equations with basic variables and 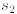. Here the basic
solution is unrealizable. If you decide to participate only in the basic activities (making deluxe
belts and having leftover labor), you must make 40 belts and have -20 leftover hours (i.e., use 20
more than you have), which you can't do within your current resources.

Exercise 8 Consider the system of equations

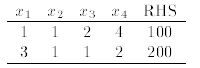
where the first four columns on the left represent a Regular mixture of nuts, a Deluxe mixture, a
small can of Premium mixture , and a large can of Premium.

a) Solve the system with and basic.

b) You want 100 cans of mixed nuts, each of which contains 1 lb cashews and 2 lb peanuts (i.e.,
you want the right-hand side of the above equation). How can you get them by blending 10
small cans of Premium with proper amounts of the Regular and Deluxe blends? Hint. Set
= 10 and 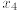= 0 in the expression for the solution values of , found in (a).

c) How can you obtain a small can of Premium mix by combining (and decombining) the Regular
and Deluxe blends?

d) How can you obtain one can of Regular mix by combining large and small cans of Premium?
If you cannot do it, why not? Hint. It has to do with linear dependence.

Exercise 9 A can of paint A has 1 quart red, 1 quart yellow. A can of paint B has 1 quart red, 1
quart blue. A can of paint C has 1 quart yellow, 1 quart blue.

a) How much of each paint must be mixed to obtain a mixture of 1 quart red, 1 quart yellow and
1 quart blue?

b) How much of each paint must be mixed to obtain one quart of pure red? What do you conclude
about the physical feasibility of such a mixture?

Exercise 10 An eletronics plant wants to make stereos and CB's. Each stereo requires 1 power
supply and 3 speakers. Each CB requires 1 power supply and 1 speaker. 100 power supplies and
200 speakers are in stock. How many stereos and CB's can it make if it wants to use all the power
supplies and all but 10 of the speakers? Hint. Use the following equations.

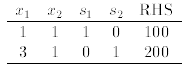
Exercise 11 A construction foreman needs cement mix containing 8 cubic yards (yd3) cement, 12
yd3 sand and 16 yd3 water. On the site are several mixer trucks containing mix A (1 yd3 cement,
3 yd3 sand, 3 yd3 water), several containing mix B (2 yd3 cement, 2 yd3 sand, 3 yd3 water) and
several containing mix C (2 yd3 cement, 2 yd3 sand, 5 yd3 water).

How many truckloads of each mix should the foreman combine to obtain the desired blend?

1.4 Inverse of a Square Matrix

If A and B are square matrices such that AB = I (the identity matrix), then B is called the inverse
of A and is denoted by A-1. A square matrix A has either no inverse or a unique inverse A-1.
In the first case, it is said to be singular and in the second case nonsingular. Interestingly, linear
independence of vectors plays a role here: a matrix is singular if its columns form a set of linearly
dependent vectors, and it is nonsingular if its columns are linearly independent. Another property
is the following: if B is the inverse of A, then A is the inverse of B.

Exercise 12 (a) Compute the matrix product .

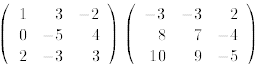(b) What is the inverse of ?

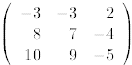(c) Show that the matrix 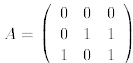is singular.

[Hint: Assume that the inverse of A is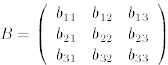and perform the matrix product
AB. Then show that no choice of 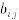 can make this product equal to the identity matrix

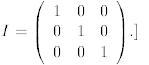
An important property of nonsingular square matrices is the following. Consider the system of
linear equations

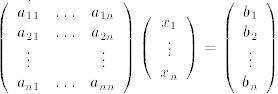, simply written as Ax = b.

When A is a square nonsingular matrix, this linear system has a unique solution, which can be
obtained as follows. Multiply the matrix equation Ax = b by A-1 on the left

A-1Ax = A-1b.

This yields Ix = A-1b and so, the unique solution to the system of linear equations is

x = A-1b.

Prev Next