Composition of Functions
Definition Given functions f and g, the composition of f with g is the function
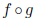de fined by
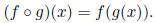
The domain of 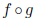is the set of values x in the
domain of g for which g(x) is in the domain
of f. In other words for x to be in the domain of
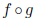we need to be able to input x into g
and then input the result g(x) into f.
Ex 1 Let f(x) = x + 2 and g(x) = x2. Then we have
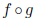()(x) = f(x2) = x2 + 2 and(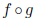)(x) = g(x + 2)
= (x + 2)2,
Since the domain of both f and g is all real numbers , this will again be the
domain of the
compositions.
Ex 2 Let f(x) =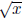
and g(x) = x2 + 1. In this case we have
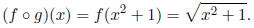
The domain of g is all real numbers . The range of g is [1,∞) which lies entirely
within the
domain of f, namely [0,∞). Then there is no need to restrict the domain of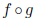
and it is
therefore (-∞,∞). On the other hand we have
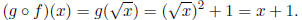
The formula x +1 has natural domain (-∞,∞). But negative numbers are not in the
domain
of f. Thus the domain of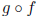 
is not the natural domain but must be restricted to
[0,∞).
Ex 3 We can often express functions as compositions of simpler functions.
Consider
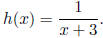
We can express h(x) as the composition of f(x) = 1/x and g(x) = x + 3:
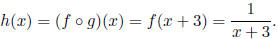
Note: There is always more than one way to do this, although in this example we
probably
chose the most obvious way.
Translations, Reflections, and Stretches
Sometimes when we compose a function f with certain basic functions the graph of
the
resulting function is related to the graph of f in a simple geometric way, such
as a translation
(vertical or horizontal shift) or a reflection across the x or y axis. We would
like to categorize
these basic operations :
Consider the graph y = f(x) for a function f and let a and c be a positive real
numbers. Here
is a table of some basic compositions and the corresponding reflects on the graph
of f(x):
Table 1. Geometric effects of basic compositions
| f(x+a) | Shifts f(x) left by a units |
| f(x-a) | Shifts f(x) right by a units |
| f(x)+a | Shifts f(x) up by a units |
| f(x)-a | Shifts f(x) down by a units |
| f(-x) | Re ects f(x) across the y-axis |
| -f(x) | Re ects f(x) across the x-axis |
| f(cx) | Stretches f(x) horizontally by a factor of 1=c |
| cf(x) | Stretches f(x) vertically by a factor of c |
Ex 4 Suppose we wish to graph the function
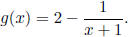
We know the basic shape of the graph of the function f(x) = 1/x. We can get from
the
graph of f to the graph of g in the following three basic steps:
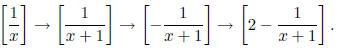
First we replaced f(x) with f(x + 1). This will shift the graph left by 1 unit.
Second we negated the entire function from step one . This is a reflection across
the x-axis.
In the last step we added 2 to the function from step two. This is a vertical
shift by 2 units.
IMPORTANT NOTE: In each step we are applying the geometric reflect to the graph of
the function in the previous step , not to the original function. Also, the order
of these steps
matters; we would have a different result if we added 2 before negating the
function.
Symmetry
Definition If a graph is unchanged by a reflection across the y-axis then this
graph is symmetric
about the y-axis. A function f with this property is called an even function.
Even
functions are functions that satisfy the condition f(x) = f(-x).
Ex 5 Some even functions: f(x) = x2 + 5, g(x) = cos(x), and h(x) = 3|x|.
Definition If a graph is unchanged by a reflection across the x-axis then this
graph is symmetric
about the x-axis. Replacing y with -y in the equation of such a graph will give
an
equivalent equation . The only function with this property is the zero function ,
f(x) = 0.
Ex 6 Some graphs with x-axis symmetry: y2 = x and x2+ y2 = 1.
Definition If a graph is unchanged by reflecting each point through the origin,
then this graph has
symmetry about the origin. A function with this property is called an odd
function.
Odd functions are functions that satisfy the condition f(-x) = -f(x).
Ex 7 Some odd functions: f(x) = x3, g(x) = sin(x), and h(x) = 1/x.
| Prev | Next |