Math 1300 FS2007 Exam
Instructions: Answer all questions and show all of your work. Answers which are not justified with appropriate work will receive 0 points. Calculators are permitted, but graphing calculators are not permitted.
Students who cheat will receive zero points on the exam and will be subject to
the university’s disciplinary procedure for academic dishonesty. Cheating
includes, but is not limited to, looking at any other student's exam, looking at
any books or notes during the exam, or using any electronic device for any
purpose other than doing arithmetic. For example, you may not use cell phones,
calculators, or any other electronic device during this exam to graph equations
or obtain mathematical formulas.
| Problem | Points Possible | Student’s Score |
| 1 | 22 | |
| 2 | 10 | |
| 3 | 8 | |
| 4 | 26 | |
| 5 | 12 | |
| 6 | 10 | |
| 7 | 12 | |
| Total | 100 |
Problem 1: The Ace Freight Company has an order for two products to be delivered to two stores of a company. The table below gives information regarding the two products.
| Product I | Product II | |
| Unit volume (cu ft) | 80 | 25 |
| Unit Weight (lb) | 100 | 30 |
Suppose that a truck can carry 2300 cu ft and 2800 lb.
(a) (6 pts) Let
x1=quantity of Product 1 the truck can carry
x2=quantity of Product 2 the truck can carry
Set up two linear equations which x1 and x2 must satisfy.

(b) (8 pts) Write the linear system from (a) as a matrix equation, and find the inverse of the coefficient matrix .

(c) (8 pts) Use the matrix equation and inverse matrix from (b) to determine how many of each product the truck can carry.

Problem 2: (10 pts) Find the value of x so that
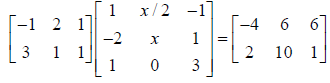
Since the (1, 2) entry is 6, we multiply (for example) the first row of the first matrix times the second column of the second matrix to obtain

Problem 3: (8 pts) Use the matrices
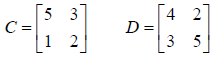
to compute5C+4D
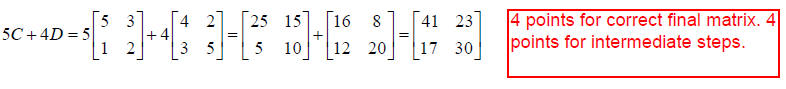
Problem 4: (a) (18 pts) Graph the following system of linear inequalities. Clearly indicate the solution region (feasible set) and find the coordinates of each corner point. Show all work in finding the coordinates of the corner points, and label each corner point with its coordinates.
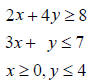
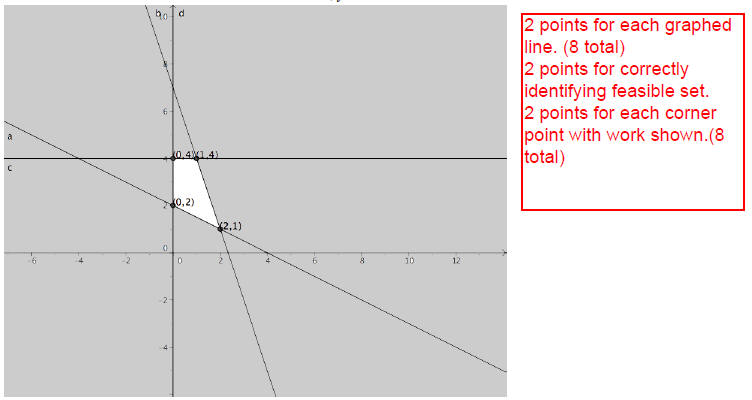
(b) (8 pts) Find the maximum value of f =4x+7y subject to the constraints given in part (a).
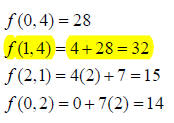

Problem 5: (12 pts) A company manufactures two types of electric hedge
trimmers, onof which is cordless. The cord-type trimmer requires 1 hour to make,
and the cordless model requires 3 hours. The company has only 800 work hours to
use in manufacturing
each day, and the packaging department can package only 300
trimmers per day. Let
x=the number of cord type models
y=the number of cordless models
Write the inequalities that describe the constraints on the number of each type of hedge trimmer produced. (You do not have to graph the solution set or optimize the objective function; this question only asks you to write the inequalities.)

Problem 6: (10 pts) How many 4-letter code words are possible using the first 10 letters of the alphabet if adjacent letters cannot be the same and the first and the last letter must be A.
To solve this problem we use the multiplication principle. We have 1 choice for the first letter, 9 choices for the second letter (it can’t be A), 8 choices for the third letter (it can’t be A and it can’t be the same as the second letter), and l choice for the fourth letter. So we have that the total number of possibilities is
1(9)(8)(1)=72

Problem 7: (12 pts) A cable television company has 8,000
subscribers in a suburban community. The company offers two premium channels,
HBO and Showtime. If 2,450 subscribers receive HBO, 1,940 receive Showtime, and
5,180 do not receive any premium channel, how many subscribers receive both HBO
and Showtime?
Let
H = the set of subscribers who receive HBO, and
S = the set of subscribers who receive Showtime.
Then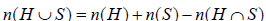 .
.
To find 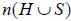 we observe that of the 8,000 subscribers, 5,180 do not receive any premium
channel . That means that 8,000 – 5,180 = 2,820 receive at least one of the
premium channels. So,
we observe that of the 8,000 subscribers, 5,180 do not receive any premium
channel . That means that 8,000 – 5,180 = 2,820 receive at least one of the
premium channels. So,
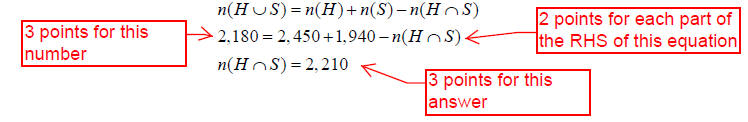
| Prev | Next |