FACTORING POLYNOMIALS AND POWER SERIES
1) Let K be complete with respect to a non-trivial non-archimedean
absolute
value | |. Is every absolute value on K (T) which extends | | equivalent to | |c
for
some
?
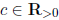2) Let K be complete with respect to a non-trivial non-archimedean absolute
value | |. Let
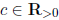and let
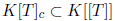denote the subset of formal sums
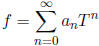
with
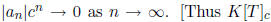is the set of power series over K which
“converge in a closed ball radius c”.] If
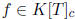define
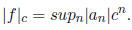
(a) Show that |f|c = 0 if and only if f = 0.
(b) Show that K[T]c is closed under addition and that
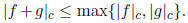
(c) Show that K[T]c is closed under multiplication and that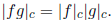
(d) Show that K[T]c is complete with respect to | |c.
(e) Show that K[T] is dense in K[T]c.
(f) If
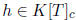and
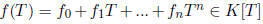satisfies
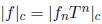
show that we can uniquely write
h = qf + r
whe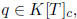re
,
where
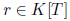has degree less than n, and where
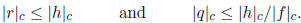
[Hint: use part (e).]
3) Which of the following polynomials are irreducible over Q5?
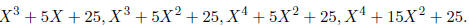
4) If p is an odd prime determine modulo p3 the monic irreducible factors of
X3 + 2pX2 + pX + p2.
5) How many roots does X3 + 25X2 + X − 9 have in Qp for p = 2, 3, 5, 7?
6) Keep the notation and assumptions of question 2). If
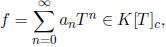
let NP(f) denote the boundary of the smallest convex set containing the points
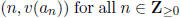and (0, y) for y any sufficiently large real number .
Suppose
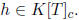Let
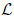denote the lowest line of slope
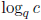which meets NP(h). Let m
denote the largest x- coordinate of a point of intersection of
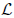with NP(h). Why
is
m an integer? Show that we can write
h = fg
where
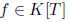is a polynomial of degree m, where
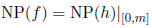
and where
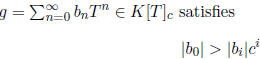
for all i > 0.
Deduce that there are only finitely many
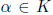with |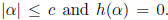
Also deduce that the number of zeros
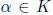with
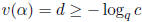is zero unless
NP(h) has a side of slope −d, in which case the number of such zeros is
positive,
but less than or equal the length of the x-axis below the side with slope −d.
7) Suppose that K is algebraically closed and complete with respect to a
nontrivial
non-archimedean absolute value | |. Also suppose that
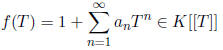
converges at all elements of K. Show that f has only finitely many zeros in any
closed ball
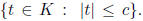Let
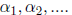be the zeros of f in K in order of
increasing absolute value. Show that
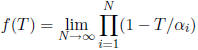
where the limit is taken with respect to any one of the absolute values | |c
with
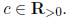Deduce that for any t ∈ K
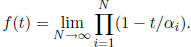
8) (a) Show that
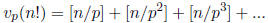
where [t] denotes the greatest integer less than or equal to a real number t.
Deduce
that
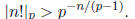
(b) If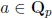 
with
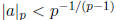and if m is a positive integer recall that
we
have
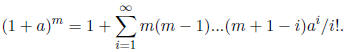
Show that this can be rewritten as
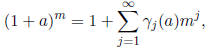
where the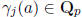 
do not depend on m and tend to zero
as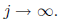 
(c) Show that X2 + X + 3 splits as (X −α )(X −β) over
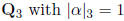and
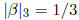. Calculate
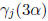mod 27
and
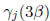mod 81
for all j.
(d) Consider the recurrence relation u(n+2) = 3u(n+1)−5u(n) with u(0) = 1
and u(1) = 2. Show that u(2m + 1) −1 mod 3 for all non- negative integers m.
Also show that
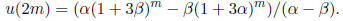
Use this to write
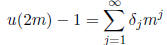
where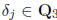
and the sum converges 3-adically for all
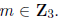. Calculate each
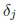
modulo 81. Show that u(2m) = 1 for at most three non-negative integers m. Find
all non-negative integers m with u(2m) = 1.
| Prev | Next |