A Math Primer
B. Addition Method
The whole problem with solving a system of
equations is that you cannot solve an equation that
has two unknowns in it. You need an equation with
only one variable so that you can isolate the variable
on one side of the equation. Both methods that we
will look at are techniques for eliminating one of the
variables to give you an equation in just one
unknown , which you can then solve by the usual
methods.
The first method of solving systems of linear
equations is the addition method, in which the two
equations are added together to eliminate one of the
variables.
Adding the equations means that we add the left
sides of the two equations together, and we add the
right sides together. This is legal because of the
Addition Principle, which says that we can add the
same amount to both sides of an equation. Since the
left and right sides of any equation are equal to each
other, we are indeed adding the same amount to both
sides of an equation.
Consider this simple example :
Example:
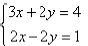
If we add these equations together, the terms
containing y will add up to zero (2y plus -2y), and we
will get
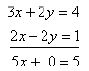
or
5x = 5
x = 1
However, we are not finished yet—we know x, but
we still don’t know y. We can solve for y by
substituting the now known value for x into either of
our original equations. This will produce an equation
that can be solved for y:
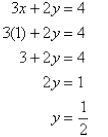
Now that we know both x and y, we can say that the
solution to the system is the pair (1, 1/2).
This last example was easy to see because of the
fortunate presence of both a positive and a negative
2y. One is not always this lucky. Consider
Example:
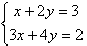
Now there is nothing so obvious, but there is still
something we can do. If we multiply the first
equation by -3, we get
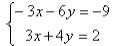
(Don’t forget to multiply every term in the equation,
on both sides of the equal sign ). Now if we add them
together the terms containing x will cancel:
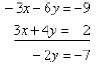
or
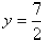
As in the previous example, now that we know y we
can solve for x by substituting into either original
equation. The first equation looks like the easiest to
solve for x, so we will use it:
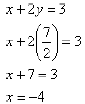
And so the solution point is (-4, 7/2).
Now we look at an even less obvious example:
Example:
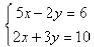
Here there is nothing particularly attractive about
going after either the x or the y. In either case, both
equations will have to be multiplied by some factor
to arrive at a common coefficient . This is very much
like the situation you face trying to find a least
common denominator for adding fractions , except
that here we call it a Least Common Multiple
(LCM). As a general rule , it is easiest to eliminate
the variable with the smallest LCM. In this case that
would be the y, because the LCM of 2 and 3 is 6. If
we wanted to eliminate the x we would have to use
an LCM of 10 (5 times 2). So, we choose to make the
coefficients of y into plus and minus 6. To do this,
the first equation must be multiplied by 3, and the
second equation by 2:
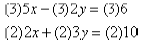
or
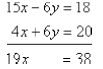
Now adding these two together will eliminate the
terms containing y:
or
x = 2
We still need to substitute this value into one of the
original equation to solve for y:
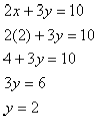
Thus the solution is the point (2, 2).
C. Substitution Method
When we used the Addition Method to solve a
system of equations, we still had to do a substitution
to solve for the remaining variable. With the
substitution method, we solve one of the equations
for one variable in terms of the other, and then
substitute that into the other equation. This makes
more sense with an example:
Example:
2y + x = 3 (1)
4y – 3x = 1 (2)
Equation 1 looks like it would be easy to solve for x,
so we take it and isolate x:
2y + x = 3
x = 3 – 2y (3)
Now we can use this result and substitute 3 - 2y in
for x in equation 2:
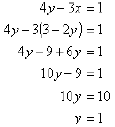
Now that we have y, we still need to substitute back
in to get x. We could substitute back into any of the
previous equations, but notice that equation 3 is
already conveniently solved for x:
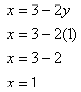
And so the solution is (1, 1).
As a rule, the substitution method is easier and
quicker than the addition method when one of the
equations is very simple and can readily be solved
for one of the variables.
| Prev | Next |