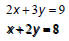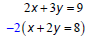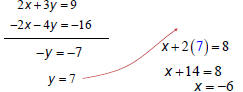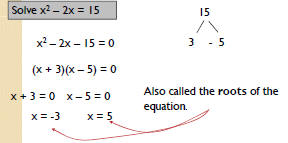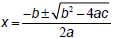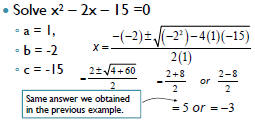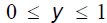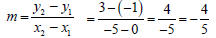GRE Review - Algebra

Objectives

• Students will be able to use the
multiplication and addition principles
together to solve linear equations

Solve for x :

3x – 2 = 10

3x = 12

x = 4

Example

3w + 4 = 5w − 6

Example

2(a − 3) = −5(2a +1)

Solving a system of linear equations

• Solve		Be sure you pay attention to what they are asking for. Sometimes they may ask: what is the value of x + y? If this is the case, you would just multiply the 2^nd equation by -1 and add; you get x + y = 1.
Mult 2^nd eq. by -2
Add

Solving Quadratics

Example

Students will be able to

• Solve equations by factoring

Example

• If the quadratic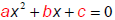

does
not factor, we will use the quadratic
formula :

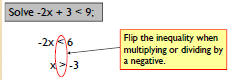
Inequalities

Example

Students should be able to

• solve linear inequalities

Double Inequalities

• They will sometimes stipulate some constraints on a
variable .

0 < y < 1

• This should be read, y is greater than 0 and less than 1. In
other words, y is between and not including or 1). If it
had been:

Then we it is everything between 0 and 1 inclusive, that is y is
between 0 and 1inlcuding 0 and 1.

Applications

• It would be impossible to cover the
myriad of applications that could be on
the test. I will go through the thought
process on just one here.

Example

• Lex is twice as far from the finish line as
he is from the start of 18 mile race. How
far has he run?

Methodology

• Step 1. Read the problem. If you don’t understand
it, read it again. If you still don’t understand it, read
it a 3rd time.

• Step 2. Identify the given information

• Step 3. Identify what you are trying to find.

• Step 4. Draw a picture if necessary to help you
visualize the problem.

• Step 5. Start labeling the drawing or setting up a
formula to solve .

• Step 6. Solve the problem.

• Step 7. Make sure your answer makes sense.

Example

• Lex is twice as far from the finish line as
he is from the start of 18 mile race. How
far has he run?

Coordinate Geometry

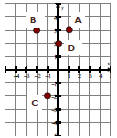
Example ( Plotting Points )

• Plot the following pairs of points
A (1, 3), B (-2, 3), C (-1, -2), D (0, 2).

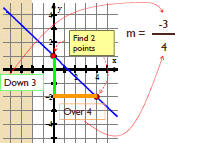
Example

Students should be able to

• find the slope when given a line or
points on the line

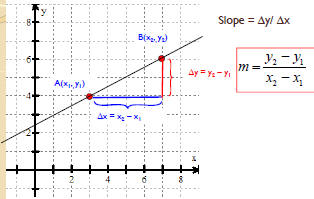
Derivation of the slope formula

Example

• Find the slope of the line containing the
points (0,-1), (-5, 3)