Linear Algebra
Linear Algebra (Spring 2005, Prof. Aitken).
Problems 1–2: Non-singular matrices. Let F be a field and let V = Fn. Let
:
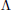Vn → F be the unique
normalized alternating n- linear functional on V . (Normalized means
).
1. Let f : Vn → F be an alternating n-linear functional. Show that if
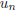is a
linear combination of
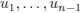then 
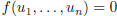. Conclude that if the columns of a
matrix are linearly dependent , then
its determinant is 0. Show that if the rows of a matrix are linearly dependent ,
then its determinant is 0.
2. Show that if a square matrix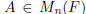 
has linear independent columns, then A
is invertible, and
detA ≠ 0. Hint: see LA10 problems 1 and 2, and LA16 problem 9. Now prove the
following:
Theorem. Let be a square matrix where F is a field. Then the
following are equivalent:
1. The matrix A is invertible. (So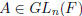 
. In other words, A is
non-singular).
2. detA ≠ 0.
3. The column vectors of A form a basis for Fn.
4. The column vectors of A are linearly independent in Fn.
5. The column vectors of A span Fn.
6. The row vectors of A form a basis of Fn.
7. The row vectors of A are linearly independent in Fn.
8. The row vectors of A span Fn.
Problems 3–6: Cramer’s Rule. Now we know that detA ≠ 0 is equivalent to A being
invertible, if the scalars
are a field F. But what if the scalars are a commutative ring? The answer is
that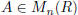 
is invertible
if and only if detA is a unit in R. In order to show this, we need Cramer’s
Rule, which is an important idea
even over fields. Let V = Rn where R is a commutative ring, and let f : V → V be
invertible. Cramer’s
rule is a technique to find f -1(u) of a vector u ∈ V if f is invertible.
3. Explain how the problem of finding f -1(u) is related to solving n linear
equations in n unknowns:
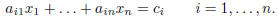
Conclude that Cramer’s rule can be understood as a technique for solving linear
equations.
4. Let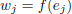 
and suppose f is invertible. Show
that if 
then
.
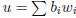Show that 
and prove
the following
Theorem (Cramer’s Rule). Let V = Rn where R is a commutative ring, and let
: Vn
→ R be the
normalized alternating n-linear functional for V . Assume that f : V → V is
linear and invertible with
matrix A. Then if u ∈ V , the preimage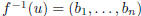 
is given by the
formula
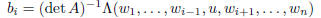
where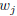 
is the jth column of A and u is put in the ith slot.
5. Suppose that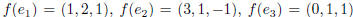 
. (Assume
R = Q if you wish). Use
Cramer’s rule to find a vector v such that f(v) = (0, 2, 1). (Optional: now find
it with row operations ).
6. A very important special case is computing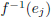 
since it gives the matrix
for f -1. Prove the following.
Use the theorem to find the matrix for f -1 where
.
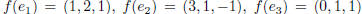Assume R = Q if you wish. (Optional: now find it using row reduction ).
Theorem ( Inverse formula ). Let V = Rn where R is a commutative ring. Also,
assume that : Vn → R
is the normalized alternating n-linear functional for V . Finally assume that f
: V → V is linear and
invertible with matrix A and inverse matrix B. Then
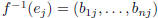is given by the formula
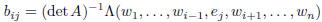
where 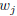is the jth column of A and
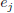is put in the ith slot. Also
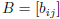is the matrix for f -1 : V → V
(so B = A -1). Thus A -1 can be computed with determinants.
| Prev | Next |