Rational Expressions Review
Recall: A rational number is any number that can be
expressed in the form a/b where a and b are
integers with b not zero .
A rational expression is an expression p/Q where P and Q are polynomials.
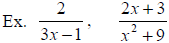
Where is a rational expression undefined?
Where is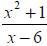 
undefined? Recall: Any fraction
is undefined when the denominator is 0. So we must
find the value for x that makes the denominator 0 to see where the rational
expression is undefined.
x – 6 = 0 x = 6 So the expression is undefined for x = 6
Where is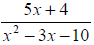 
undefined?
Solve x 2 – 3x – 10 = 0
(x – 5)(x + 2) = 0
x – 5 = 0 or x + 2 = 0 The rational expressions is undefined
when x = 5 or x = – 2
What about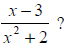
If we
try to solve x2 + 2 = 0, we see that there is no solution. Thus, this
expression is defined for all real numbers since there is no real number value
for x that makes the
denominator 0.
Simplifying Rational Expressions
Property :
Multiplying or dividing both the numerator and denominator by the same nonzero
quantity will not
change the value . (Just like with regular fractions)
Rule : To reduce a rational expression to lowest
terms, factor the numerator and denominator
completely and divide out any factors they have in common.
Examples: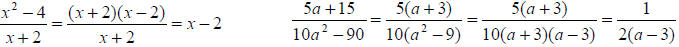 
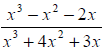Factor the numerator : x(x2 – x –
2) = x(x – 2)(x + 1)
Factor the denominator: x(x2 + 4x + 3) = x(x + 3)(x + 1)
So we have: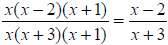 
When factors are opposites
Consider: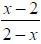
The numerator
and denominator are not the same. Note − (2 – x) = − 2 + x = x – 2
So the numerator and denominator are opposites. We can write the rational
expression as:
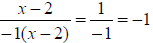
Simplify: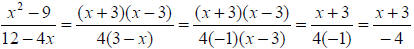
Multiplication and Division
Recall: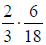
When we
multiply fractions, we factor and divide out common factors .
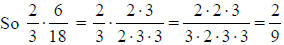
We do the same with rational expressions except we may be factoring polynomials
as well as numbers.
Example: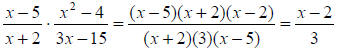
Example: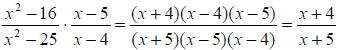
Division
Recall: Dividing by a number is the same as multiplying by its
reciprocal
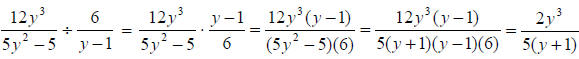
Exercises for Chapter 6 Review
Reduce the following rational expressions to lowest terms. State any
restrictions on the variable.
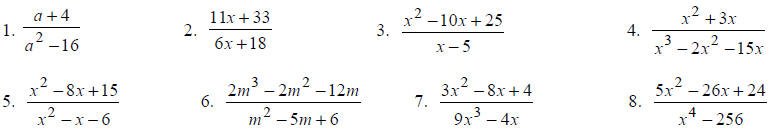
Reduce the following rational expressions to lowest terms.
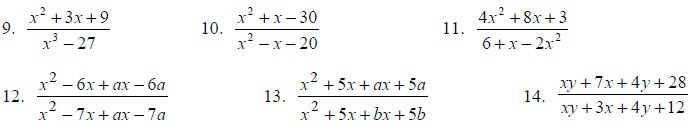
Multiply or divide as indicated.
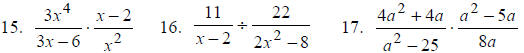
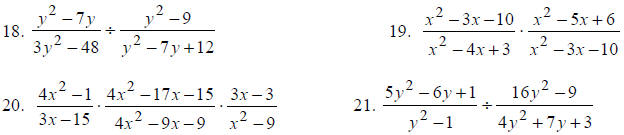
Solutions for Chapter 6 Review Exercises
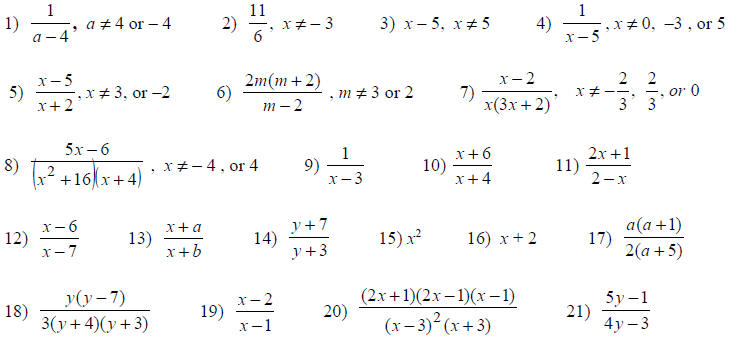
| Prev | Next |