Practice Test 1

Exam Topics

1. De nitions:
(a) Vector Space
(b) Linear Transformation
(c) Linear Independence /Dependence
(d) Linear Combination
(e) Matrix-vector and Matrix- matrix multiplication
(f) Domain, codomain, null space, range, column space, nullity, rank,
span
2. (2 × 2) Rotation Matrices
3. Elementary Row Operations /Elementary Matrices
4. Systems of Linear Equations/Solution by Row Reduction (including
existence and uniqueness of solutions )
5. REF vs. RREF
6. Matrix Inversion, Theorem 2.6

Practice Test

1. Is the given transformation linear ? Why or why not?

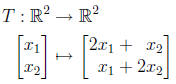
Yes

2. Let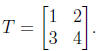

(a) Is T invertible? Why or why not? --- Yes, it's 2 × 2 and one
column is not a multiple of the other .
(b) Are the columns of T linearly independent ? Why or why not? ---
Yes, because it's invertible
(c) What is the rank of T? --- 2
(d) What is the nullity of T? --- 0
 

3. Let 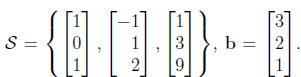Write b as a linear combi -
nation of the vectors in S.

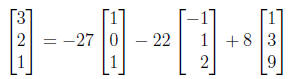
4. Give the general solution in vector form to the equation Ax = b, where

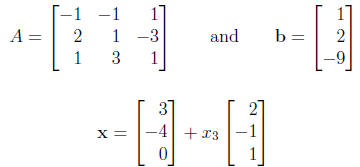
(a) Is A one-to-one? --- no
(b) Is A onto? --- no
(c) What is rank(A)? --- 2
(d) What is nullity(A)? --- 1
(e) Are the columns of A linearly independent ? --- no

5. Determine if the following vectors are linearly independent :

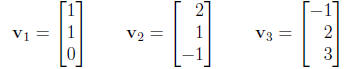
No|row reduction would give two pivots, or v₃ = 5v₁ × 3v₃

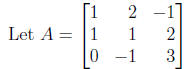
(a) Is A invertible? --- No - it has only two pivots (see above)
(b) What is rank(A)? --- 2
(c) What is nullity(A)? --- 1

6. Let 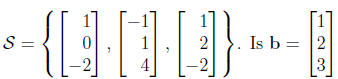in the span of S?
Yes, via row row reduction of the corresponding augmented matrix.

(a) What is the span of S? --- The row reduction above gives three
pivots, thus the span is R^3
(b) If 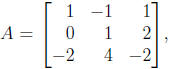is A invertible? --- Yes, every column is
a pivot column.
(c) What are rank(A) and nullity(A)? --- rank(A) = 3, nullity(A) = 0

7. Find the inverse of

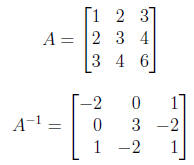
Use A^-1 to solve the system of equations

x₁ + 2x₂ + 3x₃ = 1
2x₁ + 3x₂ + 4x₃ = 2
3x₁ + 4x₂ + 6x₃ = 3

If Ax = b, then x = A^-1b, so

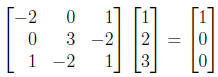
8. Suppose

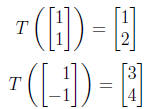
Give a matrix representing T.

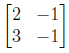
(a) Are the columns of T linearly independent ? --- Yes, the matrix is
2 × 2 and one column is not a multiple of the other.
(b) What are the rank and nullity of T? --- 2,0
(c) Is T invertible? Why or why not? --- Yes, the columns are linearly
independent.

9. Show that the inverse of

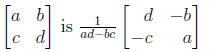
Use the row reduction method