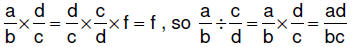Multiplying and Dividing Fractions
| 6.3 Multiplying and Dividing Fractions | |||
| 6.3.1. Modeling multiplication of fractions | |||
| 6.3.1.1. Repeated
addition can be used when we have a whole number times a rational number: 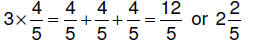 |
|||
| 6.3.1.2. Joining of
equal-sized groups can be used when we have a mixed number times a rational number :  see figure 6.12, p.
326 see figure 6.12, p.
326 |
|||
| 6.3.1.3. Area model can
also be used for multiplying a mixed number times a rational number:  see figure 6.13, p. 326 see figure 6.13, p. 326 |
|||
| 6.3.1.4. Additionally
the area model can be used to show multiplication of a rational number times a rational number. |
|||
| 6.3.1.5. Your turn p. 327: Do the practice and reflect | |||
| 6.3.2. Multiplying fractions | |||
| 6.3.2.1. Fraction with a numerator of one is called a unit fraction | |||
| 6.3.2.2. Generalization
about multiplying rational numbers represented by unit fractions: For rational numbers 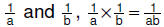 |
|||
| 6.3.2.3. Procedure for
multiplying rational numbers in fraction form: For rational numbers 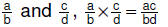 |
|||
| 6.3.2.4. Your turn p. 329: Do the practice and reflect | |||
| 6.3.2.5. Class
demonstration using paper folding to show multiplication of rational numbers: |
|||
6.3.2.5.1.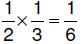 half
OF a third half
OF a third |
|||
6.3.2.5.2.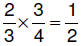 two-thirds
OF three-fourths two-thirds
OF three-fourths |
|||
6.3.2.5.3.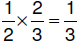 half
OF two-thirds half
OF two-thirds |
|||
6.3.2.5.4.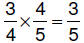 three-fourths
OF four-fifths three-fourths
OF four-fifths |
|||
| 6.3.2.6. Integer rod steps (always use least number of rods possible) | |||
| 6.3.2.7.
Class demonstration using integer rods to show multiplication of
rational numbers: |
|||
| 6.3.2.7.1. | |||
6.3.2.7.2. |
|||
6.3.2.7.3.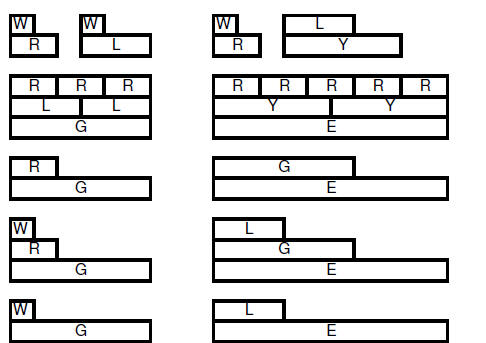 |
|||
6.3.2.7.4. |
|||
| 6.3.3. Properties of rational number multiplication | |||
| 6.3.3.1. Basic properties of rational numbers | |||
| 6.3.3.1.1. Multiplicative inverse ( reciprocal ) analogous to additive inverse property | |||
| 6.3.3.2. Your turn p. 330: Do the practice and reflect | |||
| 6.3.3.3. Basic properties for multiplication of rational numbers | |||
• Closure property: For
rational numbers 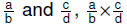 is a unique
rational is a unique
rationalnumber |
|||
• Identity property: A
unique rational number, 1, exists such that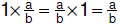 ; 1 is the multiplicative identity
element ; 1 is the multiplicative identity
element |
|||
• Zero property : For
each rational number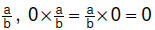 |
|||
• Commutative property:
For rational numbers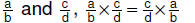 |
|||
• Associative property:
For rational numbers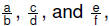 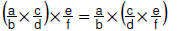 |
|||
• Distributive property:
For rational numbers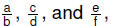 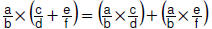 |
|||
| • Multiplicative
inverse: For every nonzero rational number b/a , a unique rational number, a/b , exists such that 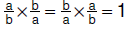 |
|||
| 6.3.3.4.
Property for multiplying an integer by a unit fraction: For any integer
a and any unit fraction 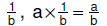 |
|||
| 6.3.3.5.
Using the properties to verify (prove) the procedure for multiplication
of rational numbers: see p. 331 |
|||
| 6.3.4. Modeling Division of fractions | |||
| 6.3.4.1. used to separate a quantity into groups of the same size | |||
| 6.3.4.2. no remainders in division of rational numbers | |||
| 6.3.4.3. Partition model – fig. 6.16 p. 332 | |||
| 6.3.4.4. Measurement model – fig.6.17 p. 332 | |||
| 6.3.4.5. Integer rod steps (always use least number of rods possible) | |||
| 6.3.4.6. Class demonstration using integer rods to show division of rational numbers: | |||
| 6.3.4.6.1. | |||
6.3.4.6.2.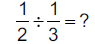 |
|||
6.3.4.6.3.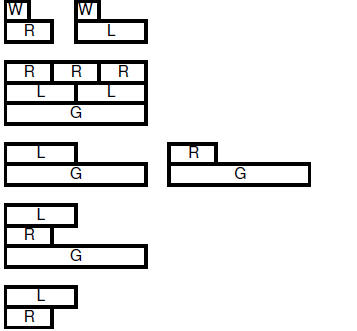 |
|||
| 6.3.4.6.4. 3/2 | |||
6.3.4.6.5.
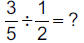 |
|||
6.3.4.6.6.
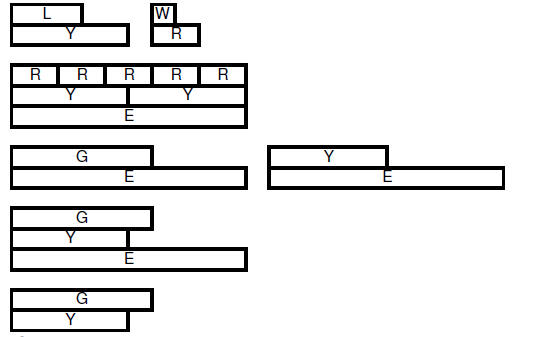 |
|||
| 6.3.4.6.7. 3/10 | |||
| 6.3.5. Definition and properties of rational number division | |||
| 6.3.5.1.
Definition of rational number division in terms of multiplication : for
rational numbers 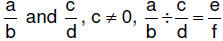 if and only if e/f is a unique
rational number such if and only if e/f is a unique
rational number suchthat 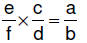 |
|||
| 6.3.5.2.
Closure property of division for nonzero rational numbers: For nonzero rational numbers 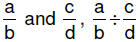 is a unique nonzero
rational number is a unique nonzero
rational number |
|||
| 6.3.6. Dividing fractions | |||
| 6.3.6.1.
Procedure for dividing fractions – multiplying by the reciprocal method :
for rational numbers a/b and c/d , where c, b, and d ≠ 0, 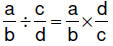 |
|||
| 6.3.6.2.
Procedure for dividing fractions – common denominator method : for
rational numbers a/b and c/d , where c ≠ 0, 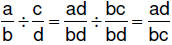 |
|||
| 6.3.6.3.
Procedure for dividing fractions – complex fraction method: for rational numbers a/b and c/d , where c ≠ 0, 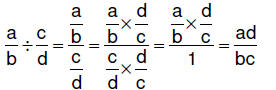 |
|||
| 6.3.6.4.
Procedure for dividing fractions – missing factor method : for rational numbers a/b and c/d , where c, b, and d ≠ 0, 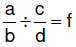 ,
where ,
where 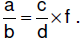 To find f, To find f,
|
|||
| 6.3.7. Estimation strategies | |||
| 6.3.7.1. rounding | |||
| 6.3.7.2. front-end estimation | |||
| 6.3.7.3. substituting compatible numbers | |||
| 6.3.7.4. Where does the decimal point go? | |||
| 6.3.7.4.1. 6.25 x 0.89 = 55625 | |||
| 6.3.7.4.2. 4.3 x 0.49 = 2107 | |||
| 6.3.7.4.3. 5.75 x 1.39 = 79925 | |||
| 6.3.8. Problems and Exercises p. 340 | |||
| 6.3.8.1. Home work: 1, 6, 7, 8, 9ac, 10, 14, 15, 16, 17, 18 | |||
| Prev | Next |