Composition of Functions

1. If 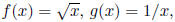and k(x) = 3x − 5, find each of the following.

(a) f(g(x))

(b) g(f(x))

(c) f(g(k(x)))

(d) k(k(x))

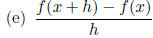
2. How many ways can you find to decompose the function

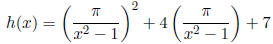
into functions f and g such that f(g(x)) = h(x)? For each possibility, list f and g.

3. Currency traders often move investments from one country to another in order to make
a profit. The following table gives exchange rates for US dollars, Japanese yen, and the
European Union’s euro on April 23, 2001.

Amount invested	Dollars purchased	Yen purchased	European euro purchased
1 dollar	1.0000	121.17	1.1157
1 yen	0.0083	1.0000	0.0092
1 euro	0.8963	108.61	1.0000

For example, one US dollar purchases 121.17 Japanese yen or 1.1157 European euros. Similarly,
one European euro purchases 108.61 Japanese yen or 0.8963 US dollars. Suppose

f(x) = Number of yen one can buy with x dollars
g(x) = Number of euros one can buy with x dollars
h(x) = Number of euros one can buy with x yen

(a) Find formulas for f , g, and h.

(b) Evaluate h(f(1000)) and interpret this in terms of currency .

4. A function f has an inverse if there exists a function g such that

f(g(x)) = g(f(x)) = x.

We usually write f⁻¹ instead of g.

Important! f⁻¹ does not mean 1/f(x).

Let f be given by the following table.

Complete the following table.

Can you find algebraic formulas related to f and f⁻¹?