Quadratic Functions
A quadratic function has the form f(x) = ax^2 + bx + c (a
≠ 0). The graph of a quadratic
function is a parabola. If a > 0 the parabola opens upward (concave up)
and if a < 0 it
opens downward (concave down)
Vertex:
The vertex is the turning point of the parabola. Its
x- coordinate is -b/2a. Its y-coordinate is
given by
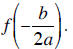
x- Intercepts (if any):
x-Intercepts (if any):
These occur when f (x) = 0; that is, when 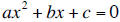
Solve this equation for x by either factoring or using the
quadratic formula. The x-intercepts
are given by
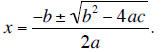
If the discriminant 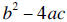 is positive, there are two x-intercepts. If it is zero, there is a
is positive, there are two x-intercepts. If it is zero, there is a
single x-intercept (at the vertex). If it is negative , there are no x-intercepts
(so the
parabola doesn ’t touch the x-axis at all).
y-Intercept:
This occurs when x = 0, so y = a(0)2 + b(0) + c = c
Symmetry:
The parabola is symmetric with respect to the vertical line through the
vertex, which is the line
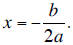
Quadratic Regression Curve :
In Section 1.5 we saw how to fit a regression line to a collection of data
points. Here, we
use technology to obtain the quadratic regression curve associated with a
set of points.
The quadratic regression curve is the quadratic curve
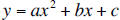 that best fits the
that best fits the
data points in the sense that the associated sum -of-squares error (SSE—see
Section 1.5)
is a minimum. Although there are algebraic methods for obtaining the quadratic
regression curve, it is normal to use technology to do this.
Problem 1.- The Better Baby Buggy Co. has just come
out with a new model, the Turbo.
The market research department predicts that the demand equation for Turbos is
given by
q = −2p + 320, where q is the number of buggies it can sell in a month if the
price is $p
per buggy. At what price should it sell the buggies to get the largest revenue?
What is the
largest monthly revenue?
Problem 2.- The average weight of an SUV could be
approximated by
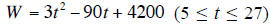 where t is its year of manufacture (t = 0
represents
where t is its year of manufacture (t = 0
represents
1970) and W is the average weight of an SUV in pounds. Sketch the graph of W as
a
function of t. According to the model, in what year were SUVs the lightest? What
was
their average weight in that year?
Problem 3.- You operate a gaming website, where
users must pay a
small fee to log on . When you charged $2 the demand was 280 log-ons per month.
When
you lowered the price to $1.50, the demand increased to 560 log-ons per month.
a. Construct a linear demand function for your website and
hence obtain the monthly
revenue R as a function of the log-on fee x.
b. Your Internet provider charges you a monthly fee of $30
to maintain your site. Express
your monthly profit P as a function of the log-on fee x, and hence determine the
log-on
fee you should charge to obtain the largest possible monthly profit. What is the
largest
possible monthly profit?
Problem 4.- The following table shows the value of
U.S. trade with China in 1994, 1999,
and 2004 (t = 0 represents 1994).
| Year t | 0 | 5 | 10 |
| China Trade ($ Billion) | 50 | 95 | 275 |
Find a quadratic model for these data, and use your model
to estimate the value of U .S.
trade with China in 2000.
| Prev | Next |