CAAP Math Homework
1. (a) Let 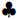 be a binary operation defined
for real numbers; this means that for any real
be a binary operation defined
for real numbers; this means that for any real
numbers x and y , we have some definition of x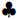 y.
y.
We say that the operation 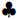 is commutative if for all real numbers x and y,
is commutative if for all real numbers x and y,
x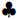 y = y
y = y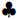 x.
x.
We say that the operation 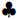 is associative if for all real numbers x, y, and
z,
is associative if for all real numbers x, y, and
z,
x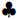 (y
(y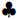 z) = (x
z) = (x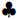 y)
y)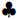 z.
z.
In the following questions, if the answer is "no", then give a
counterexample. a pair
of numbers that shows that the operation is not commutative , or three numbers
that show that the operation is not associative.
(b) Is addition of real numbers commutative?
(c) Is multiplication of real numbers commutative?
(d) Is subtraction of real numbers commutative?
(e) Is division of nonzero real numbers commutative?
(f) Is addition of real numbers associative?
(g) Is multiplication of real numbers associative?
(h) Is subtraction of real numbers associative?
(i) Is division of nonzero real numbers associative?
(j) Define the operation 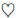 on the nonzero integers by
on the nonzero integers by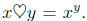 Is
Is
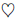 commutative? Is it associative?
commutative? Is it associative?
(k) Define the operation  on the integers by
on the integers by 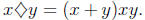 Is
Is
 commutative? Is
commutative? Is
it associative?
(l) Is it true that x y = 0 if and only if x = 0 or y = 0? If not, what is the
condition on
y = 0 if and only if x = 0 or y = 0? If not, what is the
condition on
x and y given by x y = 0? (Give an exact characterization of when this happens,
y = 0? (Give an exact characterization of when this happens,
not just some examples.)
2. Factor the polynomial x^2 + 1000002x + 2000000.
3. Try to reduce each fraction to lowest terms .
(a) Convert the decimal 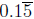 to a fraction .
to a fraction .
(b) Convert the decimal 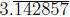 to a fraction.
to a fraction.
(c) Convert the decimal 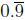 to a fraction.
to a fraction.
4. What is 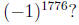
5. Use long division of polynomials to compute the quotient and the remainder of
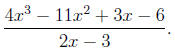
6. Starting with the curve defined by 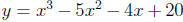 we
apply the transformation
we
apply the transformation
that shifts to the right by 1 unit. Which of the following is the equation of
the resulting
curve?
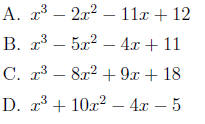
| Prev | Next |