QUADRATIC FUNCTIONS
PROTOTYPE:
The leading coefficient a ≠ 0 is called the shape parameter.
SHAPE- VERTEX FORMULA
One can write any quadratic function (1) as
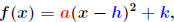(Shape-Vertex Formula)
where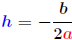
and
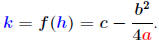
EXAMPLE 1.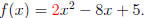 
To derive the Shape-Vertex Formula for f (x) we first identify the coeffi-
cients:
a = 2, b = -8, c = -1.
With these identifications we have:
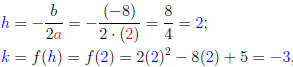
so the Shape-Vertex Formula for f(x) is:
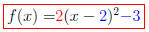
FACTS ABOUT THE GRAPH:
A. The graph has same shape as the graph of ax2, but shifted. The shift-
ing is determined by the numbers h and k that appear in the Shape-Vertex
Formula.
We illustrate this fact with Example 1
above. In that example we started with
the function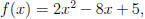 
and we
found the Shape-Vertex Formula to be
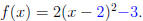
By the above Fact, we then know that the
graph of f(x) is the same as the graph of
y = 2x2, but shifted 2 units to the right,
and 3 units down.
The graph of f(x) is shown in red, while
the graph of y = 2x2 is shown in blue.
B. The shape of the graph of f(x) = ax2 + bx + c is called
a parabola.
The parabola opens upward or downward, depending on the sign of the leading
coefficient a , as shown below.
THE VERTEX. The "tip" of the parabola, marked by V in the
above
pictures, is called the vertex. Its coordinates are the numbers (h; k), given in
the Shape-Vertex Formula. The vertical line through the vertex is an axis of
symmetry for the parabola.
The vertex is a "turning point" (a point where the graph changes direction ).
Moreover:
• if a > 0, then the vertex is a minimum point;
• if a < 0, then the vertex is a maximum point.
The intervals of monotonicity (where the function is increasing or decreas-
ing) are (-∞, h) and (h,∞).
GRAPHING AND ANALYZING THE FUNCTION
Use the following steps when dealing with a quadratic function
f(x) = ax2 + bx + c:
Step 1. Find the y-intercept f(0).
Step 2. Find the x-intercept(s), by solving the equation
f(x) = 0.
Step 3. Find the coordinates of the vertex:
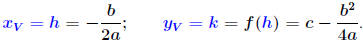
Step 4. Draw the graph. (Use the information from Steps
1-3.)
Step 5. Analyze the graph and extract information about the function.
- specify whether the vertex is a maximum or a minimum point;
- indicate the intervals where the function is increasing or decreasing.
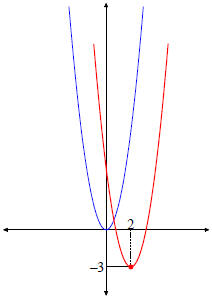
EXAMPLE. Graph and analyze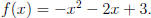
Solution: Step 1. The y-intercept is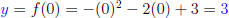 
Step 2. The x-intercept(s) are found by solving the equation:
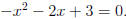
Using the Quadratic Formula, the solutions are
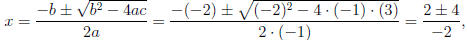
so there are two x- intercepts :
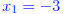and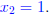 
Step 3. We find the numbers h, k:
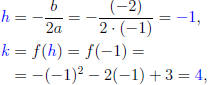
so the vertex is the point (-1, 4).
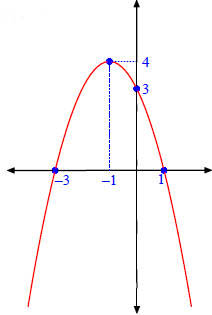
Step 4. The graph is shown on the
right.
Step 5. The vertex (-1, 4) is a maximimum point.
The function f(x) is:
• increasing on (-∞,-1);
• decreasing on (-1,∞).
FINDING THE FUNCTION, GIVEN THE VERTEX
When the vertex of the graph is given, we proceed as follows.
Step 1. Replace h, k in the Shape-Vertex Forumula
so that we get a "preliminary" form of the function:
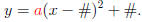
(Here it is understood that # mean concrete numbers.
Step 2. Replace x and y by the coordinates of the other point given, so
that now we would get something like :
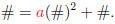
Think of the above as an equation with a as the unknown, ans solve for a.
Step 3. Replace a in the "preliminary" equation.
EXAMPLE. Find the quadratic function whose graph has
vertex (-1, 2)
and passes through the point (1, 10).
Solution: Here the vertex gives h = -1 and k = 2.
Step 1. The preliminary equation is
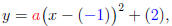
which is the same as
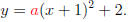
Step 2. We replace x = 1 and y = 10, and we get
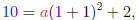
which leads to the equation
10 = 4a + 2.
We obviously get a = 2.
Step 3. The function is then given by
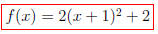
APPLIED PROBLEMS.
The meaning of the vertex, as the maximum or minimum point for the
quadratic function, is often used to solve optimization problems.
EXAMPLE. The daily cost C of producing lamps at the ABC COmpany
is given by
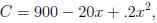
where x is the number of units produced. How many lamps should be produced
in order to yield the minimum possible cost?
Solution: What we are dealing with here is a quadratic function
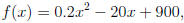
whose coefficients are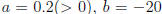 
and c = 900. What we need to
find is the value of x , for which f(x) takes the minimum value. Since a > 0,
we know that f(x) has a minimum point at the vertex. So what we need to
find is precisely the x -coordinate of the vertex, that is the h-number. So the
answer is
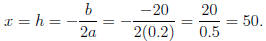
| Prev | Next |