STEPS IN FACTORING
1. Factor out the greatest common factor (GCF). (There
will not always be one).
2. Count the number of terms .
Two terms : Look to see if you have a difference of squares or a sum or
difference of cubes.
| Difference of squares : |  |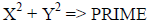
 |
|
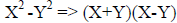| Difference of cubes : | Sum of cubes : |
 |
 |
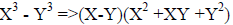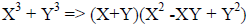Three terms : Look for two binomials.
A. Trial and error method :
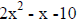*Remember! (A-C)(B+D) = AB+AD-BC-CD.
The factors of 10 take the place of C and D. The factors of
2x2 (2x and x) take the place of A and B.
Try: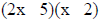
or
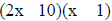
At this point, you must use trial and error to arrange the
factors and signs so that the original trinomial can be
obtained by combining the binomials in the FOIL manner.
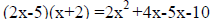combine like terms to get
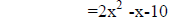
Clues for factoring trinomials by trial and error.
If the sign of the last term is +, the middle sign of the binomials will have
the same sign as the second term in the trinomial.
Example:
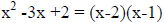or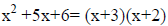
If the sign of the last term is -, the middle sign of the binomials will be +
and-.
Example:
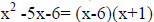or
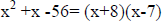
B. Grouping number method:
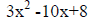1. Multiply the a term of the coefficient x2
with the constant
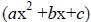c term. You are looking for two numbers that multiply
together to get 24 and add together to get 10 in this case.
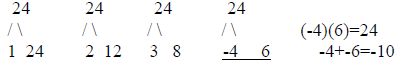
over...
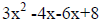2. Rewrite the
problem. Replace the middle term (bx)
with -4x and -6x.
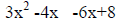3. Solve by grouping .
a. Pull out a GCF from each group .
x(3x-4) -2(3x-4)
b. Collect like groups and combine remaining terms.
(x-2)(3x-4)
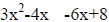3. Solve by grouping.
a. Pull out a GCF out of each group.
x(3x-4) -2(3x-4)
b. Collect like groups and combine remaining terms.
(x-2) (3x-4)
Four terms : Factor by grouping method.
A. Grouping Method
am+an+bm+b 1. Count the terms. Group the first two terms and the last
(am+an)+(bm+bn) two terms together.
a(m+n)+b(m+n) 2. Take out the common factor in the first group and the
common factor in the second group.
(m+n)(a+b) 3. Factor out the common factor.
3. Check to be sure each factor is prime, if not, repeat 1-3.
4. Check by multiplying the factors out to see if you get the original
polynomial .
REMEMBER!! FACTORING IS UNMULTIPLYING!!
| Prev | Next |